题目内容
 如图,在Rt△ABC中,∠ACB=90°,∠BAC=30°,BC=2,Rt△ABC绕点C顺时针旋转90°得Rt△EDC,连结AE,则AE的大小是( )
如图,在Rt△ABC中,∠ACB=90°,∠BAC=30°,BC=2,Rt△ABC绕点C顺时针旋转90°得Rt△EDC,连结AE,则AE的大小是( )A、2
| ||
| B、4 | ||
C、4
| ||
D、2
|
考点:旋转的性质
专题:
分析:首先利用已知条件求出AC的长,再由旋转的性质可知:AC=CE,在直角三角形ACE中利用勾股定理即可求出AE的长.
解答:解:∵在Rt△ABC中,∠ACB=90°,∠BAC=30°,BC=2,
∴AB=4,
∴AC=
=2
,
∵Rt△ABC绕点C顺时针旋转90°得Rt△EDC,
∴AC=CE=2
,
∴AE=
=
=2
,
故选D.
∴AB=4,
∴AC=
| 42-22 |
| 3 |
∵Rt△ABC绕点C顺时针旋转90°得Rt△EDC,
∴AC=CE=2
| 3 |
∴AE=
| AC2+CE2 |
| 24 |
| 6 |
故选D.
点评:本题考查的是图形旋转的性质及直角三角形的性质、勾股定理的运用,熟知图形旋转的性质是解答此题的关键,即:①对应点到旋转中心的距离相等;
②对应点与旋转中心所连线段的夹角等于旋转角;③旋转前、后的图形全等.
②对应点与旋转中心所连线段的夹角等于旋转角;③旋转前、后的图形全等.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
点(1,-2)位于( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
 如图,小红作出了边长为1的第1个正△A1B1C1,算出了正△A1B1C1的面积,然后分别取△A1B1C1三边的中点A2,B2,C2,作出了第2个正△A2B2C2,算出了正△A2B2C2的面积,用同样的方法,作出了第3个正△A3B3C3,算出了正△A3B3C3的面积…,由此可得,第2014个正△A2014B2014C2014的面积是( )
如图,小红作出了边长为1的第1个正△A1B1C1,算出了正△A1B1C1的面积,然后分别取△A1B1C1三边的中点A2,B2,C2,作出了第2个正△A2B2C2,算出了正△A2B2C2的面积,用同样的方法,作出了第3个正△A3B3C3,算出了正△A3B3C3的面积…,由此可得,第2014个正△A2014B2014C2014的面积是( )A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
如图是一个物体的三视图,则此三视图所描述物体的直观图是( )


A、 |
B、 |
C、 |
D、 |
下列事件中,属于必然事件的是( )
| A、掷一枚质地均匀的骰子,朝上一面的点数是3 |
| B、每年10月1日是我国的国庆节 |
| C、某种彩票中奖率为1%,买10000张该种彩票一定会中奖 |
| D、在一个装着白球和黑球的袋中摸球,摸出红球 |
下列说法正确的是( )
| A、调查全国青少年儿童的睡眠时间适宜采用全面调查(普查)方式 |
| B、了解全班同学本周末参加社区活动的时间适宜采用抽样调查方式 |
| C、已知一组数据:2,1,x,7,3,5,3,2的众数是2,则这组数据的中位数是2 |
| D、打开电视机,正在播放广告这一事件是不确定事件 |
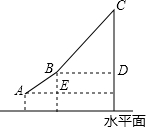 如图A、B、C表示建筑在一座比较险峻的景点上的三个缆车站的位置,已知A、B、C所处位置的海波高度分别是:130m,400m,1000m.钢缆AB与水平线AE的夹角为30°,钢缆BC与水平线BD的夹角为45°,求钢缆AB和BC的总长度.(精确到1m)
如图A、B、C表示建筑在一座比较险峻的景点上的三个缆车站的位置,已知A、B、C所处位置的海波高度分别是:130m,400m,1000m.钢缆AB与水平线AE的夹角为30°,钢缆BC与水平线BD的夹角为45°,求钢缆AB和BC的总长度.(精确到1m)