题目内容
15.计算:3$\sqrt{48}$-9$\sqrt{\frac{1}{3}}$-$\sqrt{3}$(2-$\sqrt{27}}$)-|2$\sqrt{3}$-5|.分析 先进行二次根式的乘法运算,再去绝对值,然后把二次根式化为最简二次根式后合并即可.
解答 解:原式=12$\sqrt{3}$-3$\sqrt{3}$-2$\sqrt{3}$+9+2$\sqrt{3}$-5
=9$\sqrt{3}$+4.
点评 本题考查了二次根式的混合运算:先把二次根式化为最简二次根式,然后进行二次根式的乘除运算,再合并即可.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.

练习册系列答案
相关题目
5.下列图形中,能够折叠成一个正方体的是( )
| A. |  | B. |  | C. |  | D. |  |
3.下列语句中,说法错误的是( )
| A. | 点(0,0)是坐标原点 | |
| B. | 对于坐标平面内的任一点,都有唯一的一对有序实数与它对应 | |
| C. | 点A(a,-b )在第二象限,则点B(-a,b)在第四象限 | |
| D. | 若点P的坐标为(a,b),且a•b=0,则点P一定在坐标原点 |
10.已知函数y=k(x+1)(x-$\frac{3}{k}$),下列说法正确的是( )
| A. | 方程k(x+1)(x-$\frac{3}{k}$)=-3必有实数根 | |
| B. | 若移动函数图象使其经过原点,则只能将图象向右移动1个单位 | |
| C. | 若k>0,则当x>0时,必有y随着x的增大而增大 | |
| D. | 若k<0,则当x<-1时,必有y随着x的增大而增大 |
20.若a,b是实数,且a2=$\sqrt{b-1}+\sqrt{1-b}+4$,则a+b的值是( )
| A. | 3或-3 | B. | 3或-1 | C. | -3或-1 | D. | 3或1 |
7.下列各式中,计算正确的是( )
| A. | a3•a4=a12 | B. | $\frac{x+3}{{x}^{2}-9}$=$\frac{1}{x-3}$ | C. | (a+2)2=a2+4 | D. | (-xy)3•(-xy)-2=xy |
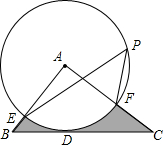 如图,△ABC中,BC=8cm,以A为圆心,以2cm为半径的圆与BC相切于点D,交AB于点E,交AC于点F,点P在圆上,∠EPF=50°,则图中阴影部分的面积为8-$\frac{10}{9}$πcm2.
如图,△ABC中,BC=8cm,以A为圆心,以2cm为半径的圆与BC相切于点D,交AB于点E,交AC于点F,点P在圆上,∠EPF=50°,则图中阴影部分的面积为8-$\frac{10}{9}$πcm2.