题目内容
6.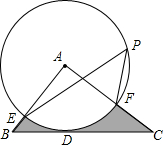 如图,△ABC中,BC=8cm,以A为圆心,以2cm为半径的圆与BC相切于点D,交AB于点E,交AC于点F,点P在圆上,∠EPF=50°,则图中阴影部分的面积为8-$\frac{10}{9}$πcm2.
如图,△ABC中,BC=8cm,以A为圆心,以2cm为半径的圆与BC相切于点D,交AB于点E,交AC于点F,点P在圆上,∠EPF=50°,则图中阴影部分的面积为8-$\frac{10}{9}$πcm2.
分析 根据圆周角定理可以求得∠A的度数,即可求得扇形EAF的面积,根据阴影部分的面积=△ABC的面积-扇形EAF的面积即可求解.
解答 解:连接AD.
∵BC是⊙A的切线,
∴AD⊥BC,
∴△ABC的面积是:$\frac{1}{2}$BC•AD=$\frac{1}{2}$×8×2=8,
∵∠A=2∠EPF=100°,则扇形EAF的面积是:$\frac{100π•{2}^{2}}{360}$=$\frac{10}{9}$π.
∴阴影部分的面积=△ABC的面积-扇形EAF的面积=8-$\frac{10}{9}$π.
故答案为8-$\frac{10}{9}$π.
点评 本题考查切线的性质,扇形面积的计算,正确求得扇形的圆心角是解题的关键,学会利用分割法求阴影部分面积,属于中考常考题型.

练习册系列答案
相关题目
1.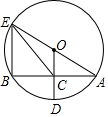 如图,⊙O中,半径OD⊥弦AB于点C,连接AO并延长交⊙O于点E,连接CE、BE,AB=8,CD=2,则EC=( )
如图,⊙O中,半径OD⊥弦AB于点C,连接AO并延长交⊙O于点E,连接CE、BE,AB=8,CD=2,则EC=( )
 如图,⊙O中,半径OD⊥弦AB于点C,连接AO并延长交⊙O于点E,连接CE、BE,AB=8,CD=2,则EC=( )
如图,⊙O中,半径OD⊥弦AB于点C,连接AO并延长交⊙O于点E,连接CE、BE,AB=8,CD=2,则EC=( )| A. | 5 | B. | 6 | C. | 3$\sqrt{5}$ | D. | 2$\sqrt{13}$ |
18.甲、乙两班学生植树造林,已知甲班每天比乙班多植5棵树,甲班植80棵树所用的天数与乙班植70棵树所用的天数相等,若设乙班每天植树x棵,则根据题意列出方程是( )
| A. | $\frac{80}{x-5}$=$\frac{70}{x}$ | B. | $\frac{80}{x}$=$\frac{70}{x+5}$ | C. | $\frac{80}{x+5}$=$\frac{70}{x}$ | D. | $\frac{80}{x}$=$\frac{70}{x-5}$ |
16. 如图所示,AB∥CD,AB∥PQ,那么∠A+∠APC+∠C等于( )
如图所示,AB∥CD,AB∥PQ,那么∠A+∠APC+∠C等于( )
 如图所示,AB∥CD,AB∥PQ,那么∠A+∠APC+∠C等于( )
如图所示,AB∥CD,AB∥PQ,那么∠A+∠APC+∠C等于( )| A. | 360° | B. | 270° | C. | 200° | D. | 180° |
 如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,O是△ABC的内心,以O为圆心,r为半径的圆与线段AB有公共点,则r的取值范围是1≤r≤$\sqrt{10}$.
如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,O是△ABC的内心,以O为圆心,r为半径的圆与线段AB有公共点,则r的取值范围是1≤r≤$\sqrt{10}$.

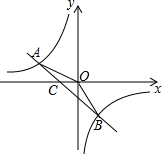 如图,已知点A(-2,1),B(1,n)是一次函数y=kx+b和反比例函数y=$\frac{m}{x}$的图象的两个交点,直线AB交x轴于点C.
如图,已知点A(-2,1),B(1,n)是一次函数y=kx+b和反比例函数y=$\frac{m}{x}$的图象的两个交点,直线AB交x轴于点C.