题目内容
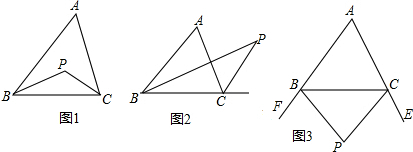
(1)如图1,若P点是∠ABC和∠ACB的平分线的交点,试证:∠P=90°+
∠A;
(2)如图2,若P点是∠ABC和外角∠ACE的平分线的交点,那么(1)中结论是否成立?若成立,请证明,若不成立,请说明理由;
(3)如图3,若P点是外角∠CBF和∠BCE的平分线的交点,那么(1)中结论是否成立?若成立,请证明;若不成立,请直接写出结论,不需说明理由.
| 1 |
| 2 |
(2)如图2,若P点是∠ABC和外角∠ACE的平分线的交点,那么(1)中结论是否成立?若成立,请证明,若不成立,请说明理由;
(3)如图3,若P点是外角∠CBF和∠BCE的平分线的交点,那么(1)中结论是否成立?若成立,请证明;若不成立,请直接写出结论,不需说明理由.

考点:三角形内角和定理,三角形的外角性质
专题:
分析:(1)利用三角形的内角和定理以及角平分线的定义即可证明;、
(2)利用三角形的外角等于不相邻的两个内角的和以及角平分线的定义即可求解;
(3)利用三角形的内角和定理以及三角形的外角的性质即可证得.
(2)利用三角形的外角等于不相邻的两个内角的和以及角平分线的定义即可求解;
(3)利用三角形的内角和定理以及三角形的外角的性质即可证得.
解答:(1)证明:∵P点是∠ABC和∠ACB的角平分线的交点,
∴∠ABP=∠PBC,∠ACP=∠PCB
∵∠A=180°-∠ABC-∠ACB=180°-2(∠PBC+∠PCB)
∠P=180°-(∠PBC+∠PCB)
∴∠P=90°+
∠A;
(2)不成立.
解:∵∠A=∠ACB-∠ABC=2∠PCE-2∠PBC=2(∠PCE-∠PBC)
∠P=∠PCE-∠PBC
∴2∠P=∠A
(3)不成立.
解:∵P点是外角∠CBF和∠BCE的平分线的交点,∠P+∠PBC+∠PCB=180°
∴∠P=180°-(∠PBC+∠PCB)
=180°-
(∠FBC+∠ECB)
=180°-
(∠A+∠ACB+∠A+∠ABC)
=180°-
(∠A+180°)
=90°-
∠A.
∴∠ABP=∠PBC,∠ACP=∠PCB
∵∠A=180°-∠ABC-∠ACB=180°-2(∠PBC+∠PCB)
∠P=180°-(∠PBC+∠PCB)
∴∠P=90°+
| 1 |
| 2 |
(2)不成立.
解:∵∠A=∠ACB-∠ABC=2∠PCE-2∠PBC=2(∠PCE-∠PBC)
∠P=∠PCE-∠PBC
∴2∠P=∠A
(3)不成立.
解:∵P点是外角∠CBF和∠BCE的平分线的交点,∠P+∠PBC+∠PCB=180°
∴∠P=180°-(∠PBC+∠PCB)
=180°-
| 1 |
| 2 |
=180°-
| 1 |
| 2 |
=180°-
| 1 |
| 2 |
=90°-
| 1 |
| 2 |
点评:本题考查的是三角形内角和定理与外角的性质,熟知三角形内角和是180°是解答此题的关键.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
下列计算中,正确的是( )
| A、-0.12=0.2 |
| B、-|-2|2=4 |
| C、(-3)3=-6 |
| D、-(-1)2n+1=1(n表示自然数) |
 阅读材料,解答问题:
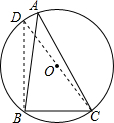
阅读材料,解答问题: 如图,以Rt△ABC的三边分别向外作三个正方形ACDE、BCNM、ABGH,其面积分别为S1,S2,S3,设Rt△ABC的两条直角边长为a,b,斜边长为c,请证明:S3=S1+S2.
如图,以Rt△ABC的三边分别向外作三个正方形ACDE、BCNM、ABGH,其面积分别为S1,S2,S3,设Rt△ABC的两条直角边长为a,b,斜边长为c,请证明:S3=S1+S2.