题目内容
 阅读材料,解答问题:
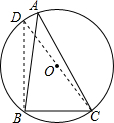
阅读材料,解答问题:如图,在锐角三角形ABC中,BC=a,AC=b,AB=c,△ABC的三个顶点都在⊙O上,且⊙O的半径为R,求证:
| a |
| sinA |
| b |
| sinB |
| c |
| sinC |
考点:圆周角定理,正弦定理与余弦定理
专题:证明题
分析:首先连接CO,并延长交⊙O于点D,由CD是直径,可得∠CBD=90°,又由圆周角定理,可得∠A=∠D,即可得sinA=sinD=
=
,则可证得
=2R,同理:
=
=2R.
| BC |
| CD |
| a |
| 2R |
| a |
| sinA |
| b |
| sinB |
| c |
| sinC |
解答: 证明:连接CO,并延长交⊙O于点D,
证明:连接CO,并延长交⊙O于点D,
∵CD是直径,
∴∠CBD=90°,
∵∠A=∠D,
∴sinA=sinD=
=
,
∴
=2R,
同理:
=
=2R,
∴
=
=
=2R.
 证明:连接CO,并延长交⊙O于点D,
证明:连接CO,并延长交⊙O于点D,∵CD是直径,
∴∠CBD=90°,
∵∠A=∠D,
∴sinA=sinD=
| BC |
| CD |
| a |
| 2R |
∴
| a |
| sinA |
同理:
| b |
| sinB |
| c |
| sinC |
∴
| a |
| sinA |
| b |
| sinB |
| c |
| sinC |
点评:此题考查了圆周角定理以及锐角三角函数的知识.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
 如图,在平行四边形ABCD中,E、F分别是AD、BC的中点,AF与BE交于点G,CE和DF交于点H,使得EF与HG互相平分,试说明理由.
如图,在平行四边形ABCD中,E、F分别是AD、BC的中点,AF与BE交于点G,CE和DF交于点H,使得EF与HG互相平分,试说明理由. 如图所示,假设学生座位到黑板的距离是5m,老师在黑板上写字,究竟要写多大,才能使学生望去时,同他看书桌上距离30cm的课本上的字0.3cm×0.2cm感觉相同(即视角相同)?
如图所示,假设学生座位到黑板的距离是5m,老师在黑板上写字,究竟要写多大,才能使学生望去时,同他看书桌上距离30cm的课本上的字0.3cm×0.2cm感觉相同(即视角相同)?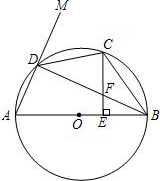 如图,AB是⊙O的直径,C是
如图,AB是⊙O的直径,C是
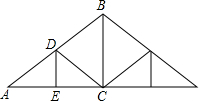 如图,是屋架设计图的一部分,点D时斜梁AB的中点,立柱BC、DE垂直于横架AC,AB=7.4m,∠A=30°,立柱BC、DE需要多长?
如图,是屋架设计图的一部分,点D时斜梁AB的中点,立柱BC、DE垂直于横架AC,AB=7.4m,∠A=30°,立柱BC、DE需要多长? 如图,A,B,C三点在⊙O上,∠A=40°,∠OCA=15°,OB,AC交于点D,则∠BDC的度数为
如图,A,B,C三点在⊙O上,∠A=40°,∠OCA=15°,OB,AC交于点D,则∠BDC的度数为 在5×5的正方形网格中,每个小格的边长均为1,把顶点是格点(即正方形的顶点)的四边形称为格点四边形.
在5×5的正方形网格中,每个小格的边长均为1,把顶点是格点(即正方形的顶点)的四边形称为格点四边形.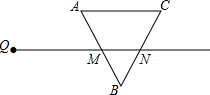 射线QN与等边△ABC的两边AB,BC分别交于点M,N,且AC∥QN,AM=MB=2cm,QM=4cm.动点P从点Q出发,沿射线QN以每秒1cm的速度向右移动,经过t秒,以点P为圆心,
射线QN与等边△ABC的两边AB,BC分别交于点M,N,且AC∥QN,AM=MB=2cm,QM=4cm.动点P从点Q出发,沿射线QN以每秒1cm的速度向右移动,经过t秒,以点P为圆心,