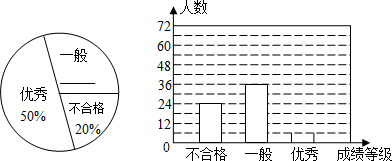
题目内容
5.请你从下列两个题中任选一个完成.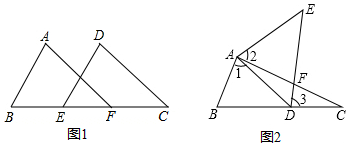
(1)如图1,点B,E,F,C在一条直线上,AB=DC,BE=CF,∠B=∠C.求证:∠A=∠D.
(2)如图2,点E在△ABC外部,点D在边BC上,DE交AC于F,若∠1=∠2=∠3,AC=AE.求证:△ABC≌△ADE.
分析 (1)先证明BF=EC,然后依据SAS证明△ABF≌△DCE,从而可得到∠A=∠D;
(2)首先依据等式的性质证明∠BAC=∠DAE,然后依据三角形的内角和定理证明∠E=∠C,最后依据ASA证明△ABC≌△ADE即可.
解答 解:(1)∵BE=CF,
∴BE+EF=CF+EF,即BF=EC.
在△ABF和△DCE中$\left\{\begin{array}{l}{AB=DC}\\{∠B=∠C}\\{BF=EC}\end{array}\right.$,
∴△ABF≌△DCE(SAS).
∴∠A=∠D.
(2)∵∠1=∠2,
∴∠BAC=∠DAE.
∵∠2=∠3,∠AFE=∠DFC,
∴∠E=∠C.
在△ABC和△ADE中$\left\{\begin{array}{l}{∠BAC=∠DAE}\\{AC=AE}\\{∠E=∠C}\end{array}\right.$,
∴△ABC≌△ADE(ASA).
点评 本题主要考查的是全等三角形的性质和判定,熟练掌握全等三角形的判定定理是解题的关键.

练习册系列答案
相关题目
16.以下列各组线段为边,能组成三角形的是( )
| A. | 2cm,3cm,5cm | B. | 5cm,6cm,10cm | C. | 1cm,1cm,3cm | D. | 2cm,4cm,8cm |
14.如果将抛物线y=ax2+bx+c向右平移2个单位,再向上平移3个单位,得到新的抛物线y=x2-2x+1,那么( )
| A. | b=6,c=12 | B. | b=-6,c=6 | C. | b=2,c=-2 | D. | b=2,c=4 |
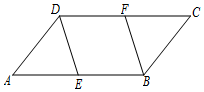 如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点,连接DE、BF.
如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点,连接DE、BF.