题目内容
13.下列计算一定正确的是( )| A. | $\sqrt{{x^2}+2x+1}=x+1$ | B. | $\sqrt{{{(-0.1)}^2}}=0.1$ | C. | $-\sqrt{{{(-\frac{1}{3})}^2}}=\frac{1}{3}$ | D. | ${(-\sqrt{3})^2}=-3$ |
分析 根据二次根式的性质,逐一化简,即可解答.
解答 解:A、$\sqrt{{x}^{2}+2x+1}$=|x+1|,故错误;
B、$\sqrt{(-0.1)^{2}}$=0.1,正确;
C、-$\sqrt{(-\frac{1}{3})^{2}}=-\frac{1}{3}$,故错误;
D、$(-\sqrt{3})^{2}$=3,故错误;
故选:B.
点评 本题考查了二次根式的性质,解决本题的关键是熟记二次根式的性质.

练习册系列答案
相关题目
6.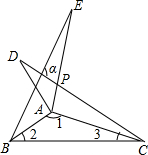 如图,△ABE、△ADC和△ABC分别是关于AB,AC边所在直线的轴对称图形,若∠1:∠2:∠3=7:2:1,则∠α的度数为( )
如图,△ABE、△ADC和△ABC分别是关于AB,AC边所在直线的轴对称图形,若∠1:∠2:∠3=7:2:1,则∠α的度数为( )
 如图,△ABE、△ADC和△ABC分别是关于AB,AC边所在直线的轴对称图形,若∠1:∠2:∠3=7:2:1,则∠α的度数为( )
如图,△ABE、△ADC和△ABC分别是关于AB,AC边所在直线的轴对称图形,若∠1:∠2:∠3=7:2:1,则∠α的度数为( )| A. | 90° | B. | 108° | C. | 110° | D. | 126° |
18.下列方程中配方中有错误的是( )
| A. | x2-4x-1=0化为(x-2)2=5 | B. | x2+6x+8=0化为(x+3)2=1 | ||
| C. | 2x2-7x-6=0化为${(x-\frac{7}{4})^2}=\frac{97}{8}$ | D. | 3x2-4x-2=0化为${(x-\frac{2}{3})^2}=\frac{10}{9}$ |
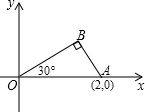 如图,将一块三角板放在平面直角坐标系中,已知∠AOB=30°,∠ABO=90°,且点A的坐标为(2,0).
如图,将一块三角板放在平面直角坐标系中,已知∠AOB=30°,∠ABO=90°,且点A的坐标为(2,0). 某校初三年级的一场篮球比赛中,如图队员甲正在投篮,已知球出手时离地面$\frac{20}{9}$m,与篮圈中心的水平距离为7m,当球出手后水平距离为4m时到达最大高度4m,篮圈距地面3m,设篮球运行的轨迹为抛物线.
某校初三年级的一场篮球比赛中,如图队员甲正在投篮,已知球出手时离地面$\frac{20}{9}$m,与篮圈中心的水平距离为7m,当球出手后水平距离为4m时到达最大高度4m,篮圈距地面3m,设篮球运行的轨迹为抛物线.