题目内容
5. 某校初三年级的一场篮球比赛中,如图队员甲正在投篮,已知球出手时离地面$\frac{20}{9}$m,与篮圈中心的水平距离为7m,当球出手后水平距离为4m时到达最大高度4m,篮圈距地面3m,设篮球运行的轨迹为抛物线.
某校初三年级的一场篮球比赛中,如图队员甲正在投篮,已知球出手时离地面$\frac{20}{9}$m,与篮圈中心的水平距离为7m,当球出手后水平距离为4m时到达最大高度4m,篮圈距地面3m,设篮球运行的轨迹为抛物线.(1)建立如图的平面直角坐标系,求此抛物线的解析式;
(2)此球能否准确投中?
(3)此时,若对方队员乙在甲前面1m处跳起盖帽拦截,已知乙的最大摸高为3.1m,那么他能否获得成功?
分析 (1)根据抛物线的顶点坐标及球出手时的坐标,可确定抛物线的解析式;
(2)令x=7,求出y的值,与3m比较即可作出判断;
(3)将x=1代入y=-$\frac{1}{9}$(x-4)2+4得y=3进而得出答案.
解答 解:(1)根据题意,球出手点、最高点和篮圈的坐标分别为:
A(0,$\frac{20}{9}$),B(4,4),C(7,3)
设二次函数解析式为y=a(x-h)2+k,
将点(0,$\frac{20}{9}$)代入可得:16a+4=$\frac{20}{9}$,
解得:a=-$\frac{1}{9}$,
∴抛物线解析式为:y=-$\frac{1}{9}$(x-4)2+4;
(2)将C(7,3)点坐标代入抛物线解析式得:
∴-$\frac{1}{9}$(7-4)2+4=3
∴左边=右边
即C点在抛物线上,
∴此球一定能投中.
(3)能拦截成功.
理由:将x=1代入y=-$\frac{1}{9}$(x-4)2+4得y=3
∵3<3.1
∴他能拦截成功.
点评 解答本题的关键是利用待定系数法求出抛物线解析式,注意建立数学模型,培养自己利用数学知识解决实际问题的能力.

练习册系列答案
 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
16.已知等腰三角形一腰上的中线将它的周长分成6cm和12cm两部分,则等腰三角形的底边长为( )
| A. | 2cm | B. | 10cm | C. | 6cm或4cm | D. | 2cm或10cm |
13.下列计算一定正确的是( )
| A. | $\sqrt{{x^2}+2x+1}=x+1$ | B. | $\sqrt{{{(-0.1)}^2}}=0.1$ | C. | $-\sqrt{{{(-\frac{1}{3})}^2}}=\frac{1}{3}$ | D. | ${(-\sqrt{3})^2}=-3$ |
20.关于x的一元二次方程x2-(2m-1)x+m2-1=0的两实数根为x1,x2,且x12+x22=3,则m的值是( )
| A. | 0 | B. | 0或2 | C. | 2 | D. | 0或-2 |
17.下列计算中,正确的是( )
| A. | (-6)+(-4)=-2 | B. | -9+(-4)=-13 | C. | |-9|+9=0 | D. | -9+4=-13 |
14.王师傅购销A、B、C、D、E五种型号的机器零件,由于王师傅不太了解市场行情,在这次买卖中王师傅有赔有赚,下表记录了王师傅每种机器零件的进货数量和每个机器零件赔赚情况:
请问:在这次买卖中,王师傅是赚钱了还是赔钱了,赚或赔了多少钱.说明理由.
| 型号 | A | B | C | D | E |
| 进货数量 | 200 | 400 | 500 | 300 | 200 |
| 每个零件赔赚情况 | 赔1.5元 | 赚2元 | 赔0.5元 | 赔1元 | 赚0.2元 |
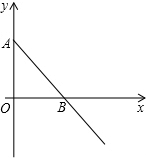 如图,在平面直角坐标系中,直线AB与y轴的正半轴交于点A,与x轴交于点B(2,0),三角形△ABO的面积为2.点Q的坐标是(4,0).动点P从点O出发,以每秒1个单位长度的速度在射线OB上运动,过P作PM⊥x轴交直线AB于M.
如图,在平面直角坐标系中,直线AB与y轴的正半轴交于点A,与x轴交于点B(2,0),三角形△ABO的面积为2.点Q的坐标是(4,0).动点P从点O出发,以每秒1个单位长度的速度在射线OB上运动,过P作PM⊥x轴交直线AB于M.