题目内容
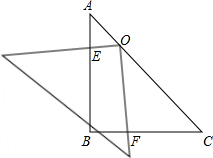 在Rt△ABC中,∠B=90°,将一块等腰直角三角板的直角顶点放在斜边AC的中点O处,将三角板绕点O旋转,三角板的两直角边分别交AB、BC或其延长线于E、F两点,若将三角板的直角顶点放在斜边上的点O处,当OC=3AO,求OE:OF的值.
在Rt△ABC中,∠B=90°,将一块等腰直角三角板的直角顶点放在斜边AC的中点O处,将三角板绕点O旋转,三角板的两直角边分别交AB、BC或其延长线于E、F两点,若将三角板的直角顶点放在斜边上的点O处,当OC=3AO,求OE:OF的值.考点:相似三角形的判定与性质
专题:
分析:分别过O作OM⊥AB,ON⊥BC,垂足分别为M、N,由条件可证得△AMO∽△ONC,△OME∽△ONF,则可知到
=
=
=
.
| OE |
| OF |
| OM |
| ON |
| AO |
| CO |
| 1 |
| 3 |
解答: 解:
解:
如图,分别过O作OM⊥AB,ON⊥BC,垂足分别为M、N,
∵∠EOF=90°,
∴∠MOE+∠EON=∠EON+∠NOF,
∴∠MOE=∠NOF,且∠OME=∠ONF,
∴△OME∽△ONF,
∴
=
,
∵∠A=∠C,且∠AMO=∠ABC=90°,
∴△AMO∽△ABC,
∴
=
=
=
,
∴
=
.
 解:
解:如图,分别过O作OM⊥AB,ON⊥BC,垂足分别为M、N,
∵∠EOF=90°,
∴∠MOE+∠EON=∠EON+∠NOF,
∴∠MOE=∠NOF,且∠OME=∠ONF,
∴△OME∽△ONF,
∴
| OE |
| OF |
| OM |
| ON |
∵∠A=∠C,且∠AMO=∠ABC=90°,
∴△AMO∽△ABC,
∴
| OM |
| ON |
| AO |
| CO |
| AO |
| 3AO |
| 1 |
| 3 |
∴
| OE |
| OF |
| 1 |
| 3 |
点评:本题主要考查相似三角形的判定和性质,利用条件构造相似三角形是解题的关键.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案
相关题目
 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D.
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D. 如图,一块梯形玻璃的下底及两腰的部分摔碎,量得∠BAD=120°,∠ADC=105°,请求出两腰的夹角∠P的度数.
如图,一块梯形玻璃的下底及两腰的部分摔碎,量得∠BAD=120°,∠ADC=105°,请求出两腰的夹角∠P的度数.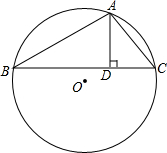 如图,已知△ABC内接于⊙O,AD是高线,已知AB=15,AC=8,AD=6,求⊙O的直径.
如图,已知△ABC内接于⊙O,AD是高线,已知AB=15,AC=8,AD=6,求⊙O的直径.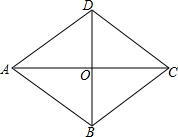 如图,有一个菱形的纸片ABCD,对角线BD=6cm,AC=8cm,从中剪出一个面积最大的圆形纸片,则这个圆的面积为
如图,有一个菱形的纸片ABCD,对角线BD=6cm,AC=8cm,从中剪出一个面积最大的圆形纸片,则这个圆的面积为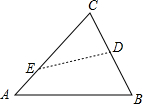 如图,点D在BC上,AC=15cm,BC=9cm,CD=3cm,一动点E在边AC上以1cm/s的速度自点A向点C移动,几秒后△ECD与△ABC相似?
如图,点D在BC上,AC=15cm,BC=9cm,CD=3cm,一动点E在边AC上以1cm/s的速度自点A向点C移动,几秒后△ECD与△ABC相似?