题目内容
 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D.
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D.(1)图中有哪两个三角形相似?
(2)求证:AC2=AD•AB;BC2=BD•BA;CD2=AD•BD;
(3)若AD=2,DB=8,求AC,BC,CD的长;
(4)若AC=6,DB=9,求AD,CD,BC的长;
(5)求证:AC•BC=AB•CD.
考点:相似三角形的判定与性质
专题:
分析:(1)由条件可知∠A=∠DCB,∠ACD=∠B,可证得△ACD∽△ABC∽△CDB;
(2)利用(1)可得到
=
,
=
,
=
,可证得结论;
(3)代入(2)中结论可求得;
(4)同(3)代入(2)可求得;
(5)利用面积相等即可得出结论.
(2)利用(1)可得到
| AC |
| AD |
| AB |
| AC |
| BC |
| BA |
| BD |
| BC |
| CD |
| AD |
| BD |
| CD |
(3)代入(2)中结论可求得;
(4)同(3)代入(2)可求得;
(5)利用面积相等即可得出结论.
解答:(1)解:∵∠ACB=90°,CD⊥AB,
∴∠ADC=∠ACB,
∴∠ACD+∠A=∠A+∠B=90°,
∴∠ACD=∠B,
∴△ACD∽△ABC,△ACD∽△CDB,
同理可证得△CDB∽△ABC,
∴相似的三角形有:△ACD和△ABC,△ACD和△CDB,△CDB和△ABC;
(2)证明:∵△ACD∽△ABC,
∴
=
,
∴AC2=AD•AB,
同理可得
=
,
=
,
∴BC2=BD•AB,CD2=AD•BD;
(3)解:∵AD=2,DB=8,
∴CD2=AD•BD=2×8=16,
∴CD=4,
又∵AB=AD+BD=10,
∴AC2=AD•AB=2×10=20,BC2=BD•AB=8×10=80,
∴AC=2
,BC=4
;
(4)解:∵AC=6,DB=9,且AB=AD+BD,
∴AC2=AD(AD+BD),即62=AD2+9AD,
解得AD=3或(-12舍去),
∴CD2=AD•BD=3×9=27,
∴CD=3
,
∴AB=AD+BD=12,
∴BC2=BD•AB=9×12=108,
∴BC=6
;
(5)证明:∵S△ABC=
AC•BC,且S△ABC=
CD•AB,
∴AC•BC=CD•AB.
∴∠ADC=∠ACB,
∴∠ACD+∠A=∠A+∠B=90°,
∴∠ACD=∠B,
∴△ACD∽△ABC,△ACD∽△CDB,
同理可证得△CDB∽△ABC,
∴相似的三角形有:△ACD和△ABC,△ACD和△CDB,△CDB和△ABC;
(2)证明:∵△ACD∽△ABC,
∴
| AC |
| AD |
| AB |
| AC |
∴AC2=AD•AB,
同理可得
| BC |
| BA |
| BD |
| BC |
| CD |
| AD |
| BD |
| CD |
∴BC2=BD•AB,CD2=AD•BD;
(3)解:∵AD=2,DB=8,
∴CD2=AD•BD=2×8=16,
∴CD=4,
又∵AB=AD+BD=10,
∴AC2=AD•AB=2×10=20,BC2=BD•AB=8×10=80,
∴AC=2
| 5 |
| 5 |
(4)解:∵AC=6,DB=9,且AB=AD+BD,
∴AC2=AD(AD+BD),即62=AD2+9AD,
解得AD=3或(-12舍去),
∴CD2=AD•BD=3×9=27,
∴CD=3
| 3 |
∴AB=AD+BD=12,
∴BC2=BD•AB=9×12=108,
∴BC=6
| 3 |
(5)证明:∵S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
∴AC•BC=CD•AB.
点评:本题主要考查相似三角形的判定和性质,掌握直角三角形中角之间的关系是解题的关键,注意方程思想的应用.

练习册系列答案
相关题目
 如图是一个几何体的三视图,则这个几何体的表面积为( )
如图是一个几何体的三视图,则这个几何体的表面积为( )| A、50π | B、100π |
| C、150π | D、175π |
下列数中最小的数是( )
| A、-3 | ||
| B、0 | ||
C、
| ||
| D、4 |
 在直角△ABC中,∠C=90°,E、F在AB上,DG分别在BD、AC上,且四边形DEFG是正方形,求证:EF2=BE•AF.
在直角△ABC中,∠C=90°,E、F在AB上,DG分别在BD、AC上,且四边形DEFG是正方形,求证:EF2=BE•AF.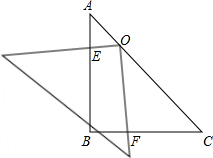 在Rt△ABC中,∠B=90°,将一块等腰直角三角板的直角顶点放在斜边AC的中点O处,将三角板绕点O旋转,三角板的两直角边分别交AB、BC或其延长线于E、F两点,若将三角板的直角顶点放在斜边上的点O处,当OC=3AO,求OE:OF的值.
在Rt△ABC中,∠B=90°,将一块等腰直角三角板的直角顶点放在斜边AC的中点O处,将三角板绕点O旋转,三角板的两直角边分别交AB、BC或其延长线于E、F两点,若将三角板的直角顶点放在斜边上的点O处,当OC=3AO,求OE:OF的值.