题目内容
若喷嘴离地面的高度为1.25m,水流喷出的高度y(m)与水平距离x(m)之间的函数关系式为y=a(x-1)2+2.25
(1)求出的水流离地面的最大高度;
(2)若把喷水池改成圆形,那么水池半径至少为多少时,才能使喷出的水流不落在水池外?
(1)求出的水流离地面的最大高度;
(2)若把喷水池改成圆形,那么水池半径至少为多少时,才能使喷出的水流不落在水池外?
考点:二次函数的应用
专题:
分析:(1)利用二次函数最值求法直接得出答案;
(2)首先求出抛物线解析式,进而得出y=0时,x的值进而得出答案.
(2)首先求出抛物线解析式,进而得出y=0时,x的值进而得出答案.
解答:解:(1)∵水流喷出的高度y(m)与水平距离x(m)之间的函数关系式为y=a(x-1)2+2.25,
∴水流离地面的最大高度为:2.25m;
(2)由题意可得:二次函数图象过点(0,1.25),
则1.25=a(0-1)2+2.25
解得:a=-1,
故y=-(x-1)2+2.25
当y=0,则0=-(x-1)2+2.25
解得:x1=2.5,x2=-0.5(不合题意舍去),
故水池半径至少为2.5m时,才能使喷出的水流不落在水池外.
∴水流离地面的最大高度为:2.25m;
(2)由题意可得:二次函数图象过点(0,1.25),
则1.25=a(0-1)2+2.25
解得:a=-1,
故y=-(x-1)2+2.25
当y=0,则0=-(x-1)2+2.25
解得:x1=2.5,x2=-0.5(不合题意舍去),
故水池半径至少为2.5m时,才能使喷出的水流不落在水池外.
点评:此题主要考查了二次函数的应用,根据题意得出抛物线解析式是解题关键.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
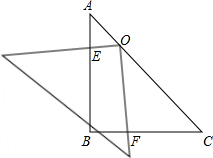 在Rt△ABC中,∠B=90°,将一块等腰直角三角板的直角顶点放在斜边AC的中点O处,将三角板绕点O旋转,三角板的两直角边分别交AB、BC或其延长线于E、F两点,若将三角板的直角顶点放在斜边上的点O处,当OC=3AO,求OE:OF的值.
在Rt△ABC中,∠B=90°,将一块等腰直角三角板的直角顶点放在斜边AC的中点O处,将三角板绕点O旋转,三角板的两直角边分别交AB、BC或其延长线于E、F两点,若将三角板的直角顶点放在斜边上的点O处,当OC=3AO,求OE:OF的值. 如图,在△ABC中,AB=AC,D是AC上一点,过D作DE⊥BC于E,与BA的延长线交于F,求证:AD=AF.
如图,在△ABC中,AB=AC,D是AC上一点,过D作DE⊥BC于E,与BA的延长线交于F,求证:AD=AF. 如图,有一张直角三角形纸片,两直角边AC=5cm,BC=10cm,将△ABC折叠,点B与点A重合,折痕为DE,求CD的长.
如图,有一张直角三角形纸片,两直角边AC=5cm,BC=10cm,将△ABC折叠,点B与点A重合,折痕为DE,求CD的长. 如图,在梯形ABCD中,AB∥CD,AD=BC,延长AB到E,使BE=DC.试判断AC与CE的大小关系?并说明理由.
如图,在梯形ABCD中,AB∥CD,AD=BC,延长AB到E,使BE=DC.试判断AC与CE的大小关系?并说明理由.