题目内容
11.已知关于x的方程x2+cx+a=0的两个整数根恰好比方程x2+ax+b=0的两个根都小2,则a+b+c的值为-8或0.分析 设出第一个方程的两根,表示出后面方程的另2根.利用根与系数的关系得到与a的关系,进而消去a,得到两个一次项的积为一个常数的形式,判断可能的整数解,得到a,b,c的值,相加即可.
解答 解:设方程x2+ax+b=0的两个根为α,β,
∵方程有整数根,
设其中α,β为整数,且α≤β,
则方程x2+cx+a=0的两根为α+2,β+2,
∴α+β=-a,(α+2)(β+2)=a,
两式相加,得αβ+3α+3β+4=0,
即(α+3)(β+3)=5,
∴$\left\{\begin{array}{l}{α+3=1}\\{β+3=5}\end{array}\right.$或$\left\{\begin{array}{l}{α+3=5}\\{β+3=1}\end{array}\right.$,
∴$\left\{\begin{array}{l}{α=-2}\\{β=2}\end{array}\right.$或$\left\{\begin{array}{l}{α=2}\\{β=-2}\end{array}\right.$,
又∵a=-(α+β)=-[(-2)+2]=0,b=αβ=-2×2=-4,c=-[(α+2)+(β+2)]=-[(-2+2)+(2+2)]=-4,
或a=-(α+β)=-[2+(-2)]=0,b=αβ=2×(-2)=-4,c=-[(α+2)+(β+2)]=-[(2-2)+(-2-2)]=4,
∴a=0,b=-4,c=-4;或者a=0,b=-4,c=4,
∴a+b+c=0+(-4)+(-4)=-8或a+b+c=0+(-4)+4=0,
综上所述,a+b+c=-8或0.
故答案是:-8或0.
点评 主要考查一元二次方程根与系数关系的应用;利用根与系数的关系得到两根之间的关系是解决本题的关键;消去a后得到两个一次项的积为一个常数的形式是解决本题的难点.

 阅读快车系列答案
阅读快车系列答案| A. | 甲地:总体平均数为3,中位数为4 | |
| B. | 乙地:中位数为2,众数为3 | |
| C. | 丙地:总体平均数为2,总体方差为3 | |
| D. | 丁地:总体平均数为1,总体方差大于0 |
| A. | x≤2 | B. | x≥2 | C. | x≥-1 | D. | -1≤x≤2 |
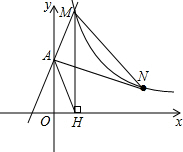 直线y=2x+2与y轴交于A点,与反比例函数y=$\frac{k}{x}$(x>0)的图象交于点M,过M作MN⊥x轴于点H,OA=2HO.
直线y=2x+2与y轴交于A点,与反比例函数y=$\frac{k}{x}$(x>0)的图象交于点M,过M作MN⊥x轴于点H,OA=2HO.