题目内容
8.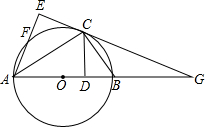 如图,在Rt△AEG中,∠E=90°,∠EAG的平分数交EG于C,过C作AC的垂线交AG于B,以AB为直径的⊙O交AE于F
如图,在Rt△AEG中,∠E=90°,∠EAG的平分数交EG于C,过C作AC的垂线交AG于B,以AB为直径的⊙O交AE于F(1)求证:EG是的切线;
(2)过C作AG的垂线,垂足为D,求证:EF=BD.
分析 (1)连接OC,如图,由AC平分∠EAG得到∠2=∠3,加上∠1=∠2,则∠1=∠3,于是可判断OC∥AE,所以OC⊥EG,然后根据切线的判定可判断EG是的切线;
(2)连接CF,根据角平分线的性质定理得到CE=CD,再利用圆内接四边形的性质得到∠EFC=∠DBC,则可证明△EFC≌△DCB,所以EF=BD.
解答 证明:(1)连接OC,如图,
∵AC平分∠EAG,
∴∠2=∠3,
∵OA=OC,
∴∠1=∠2,
∵∠1=∠3,
∴OC∥AE,
∵AE⊥EG,
∴OC⊥EG,
∴EG是的切线;
(2)连接CF,
∵AC平分∠EAG,CE⊥AE,CD⊥AB,
∴CE=CD,
∵∠CBD+∠AFC=180°,∠EFC+∠AFC=180°,
∴∠EFC=∠DBC,
在△EFC和△DCB中
$\left\{\begin{array}{l}{∠EFC=∠DBC}\\{∠E=∠BDC}\\{CE=CB}\end{array}\right.$,
∴△EFC≌△DCB,
∴EF=BD.
点评 本题考查了切线的判定:经过半径的外端且垂直于这条半径的直线是圆的切线.也考查了圆周角定理和三角形全等的判定与性质.

练习册系列答案
相关题目
19.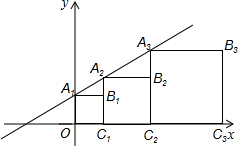 如图,坐标系中的正方形A1OC1B1,A2C1C2B2,A3C2C3B3,…的一边在x轴上,顶点A1,A2,A3,…在直线y=x+1上.
如图,坐标系中的正方形A1OC1B1,A2C1C2B2,A3C2C3B3,…的一边在x轴上,顶点A1,A2,A3,…在直线y=x+1上.
(1)将下列表格补充完整:
(2)写出第4个正方形的边长,并猜想第n个正方形的边长(用含n的代数式表示)
 如图,坐标系中的正方形A1OC1B1,A2C1C2B2,A3C2C3B3,…的一边在x轴上,顶点A1,A2,A3,…在直线y=x+1上.
如图,坐标系中的正方形A1OC1B1,A2C1C2B2,A3C2C3B3,…的一边在x轴上,顶点A1,A2,A3,…在直线y=x+1上.(1)将下列表格补充完整:
| 坐标 | A1(0,1) | A2(1, 2) | A3( 3, 4) |
| 正方形边长 | A1OC1B1:1 | A2C1C2B2: 2 | A3C2C3B3: 4 |
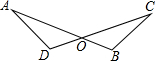 如图,已知AB与CD相交于点O,且AB=CD,当满足OB=OD时,AD=BC.(只需填出一个条件)
如图,已知AB与CD相交于点O,且AB=CD,当满足OB=OD时,AD=BC.(只需填出一个条件)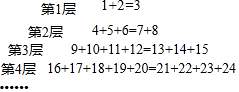 观察下列等式:在上述数字宝塔中,从上往下、从左往右数,第7层的第二个数是50,第24层最后一个数是624.
观察下列等式:在上述数字宝塔中,从上往下、从左往右数,第7层的第二个数是50,第24层最后一个数是624.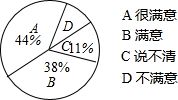 某商场为了解本商场服务质量,随机调查了来本商场的200名顾客,调查的结果如图所示,根据图中给出的信息,这200名顾客中对该商场的服务质量表示不满意的有14名.
某商场为了解本商场服务质量,随机调查了来本商场的200名顾客,调查的结果如图所示,根据图中给出的信息,这200名顾客中对该商场的服务质量表示不满意的有14名.