题目内容
6.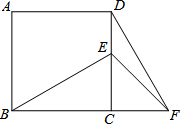 已知:如图,在正方形ABCD中,E为CD边上的一点,F为BC的延长线上一点,CE=CF.
已知:如图,在正方形ABCD中,E为CD边上的一点,F为BC的延长线上一点,CE=CF.(1)△BCE与△DCF全等吗?说明理由;
(2)若∠BEC=60°,求∠EFD.
分析 (1)根据正方形的四条边都相等,四个角都是直角,BC=CD、∠BCE=∠DCF=90°,又CE=CF,根据边角边定理即可证明△BCE和△DCF全等;
(2)由(1)可知△BCE≌△DCF得∠BEC=∠DFC=60°,可得∠EFC=45°,从而可求∠EFD的度数.
解答 证明:(1)∵四边形ABCD是正方形,
∴BC=DC,∠BCD=90°
∵F为BC延长线上的点,
∴∠DCF=90°,
∴∠BCD=∠DCF,
在△BCE和△DCF中,
$\left\{\begin{array}{l}{BC=DC}\\{∠BCD=∠DCF}\\{CE=CF}\end{array}\right.$,
∴△BCE≌△DCF(SAS);
(2)∵△BCE≌△DCF,
∴∠BEC=∠DFC=60°,
∵∠DCF=90°,CE=CF,
∴∠EFC=45°,
∴∠EFD=∠DFC-∠EFC=60°-45°=15°.
点评 本题主要考查正方形的性质,三角形全等的判定与性质,等腰三角形的性质,证明三角形全等是解决问题的关键.

练习册系列答案
相关题目
14.下列运算正确的是( )
| A. | (a-b)2=a2-b2 | B. | (a+b)2=a2+ab+b2 | C. | (1+a)(a-1)=a2-1 | D. | (a+b)(b-a)=a2-b2 |
11.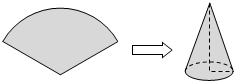 用圆心角为120°,半径为6cm的扇形纸片卷成一个圆锥形无底纸帽(如图所示),则这个纸帽的高是( )
用圆心角为120°,半径为6cm的扇形纸片卷成一个圆锥形无底纸帽(如图所示),则这个纸帽的高是( )
 用圆心角为120°,半径为6cm的扇形纸片卷成一个圆锥形无底纸帽(如图所示),则这个纸帽的高是( )
用圆心角为120°,半径为6cm的扇形纸片卷成一个圆锥形无底纸帽(如图所示),则这个纸帽的高是( )| A. | 4cm | B. | 4$\sqrt{2}$cm | C. | 3$\sqrt{2}$cm | D. | $\sqrt{2}$cm |
 对于边长为4的等边三角形ABC,建立适当的平面直角坐标系,写出各个顶点的坐标.
对于边长为4的等边三角形ABC,建立适当的平面直角坐标系,写出各个顶点的坐标.
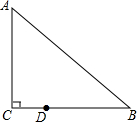 如图,在Rt△ABC中,∠C=90°,∠B=40°,点D在边BC上,BD=2CD.把△ABC绕点D逆时针旋转m度后(0<m<360),如果点B恰好落在初始Rt△ABC的边所在的直线上,那么m=100°或120°.
如图,在Rt△ABC中,∠C=90°,∠B=40°,点D在边BC上,BD=2CD.把△ABC绕点D逆时针旋转m度后(0<m<360),如果点B恰好落在初始Rt△ABC的边所在的直线上,那么m=100°或120°.