题目内容
1.等腰三角形的底边长为10,面积为$\frac{25}{3}\sqrt{3}$,则它的顶角度数是120°.分析 作等腰△ABC底边上的高AD.由△ABC的面积是$\frac{25}{3}\sqrt{3}$,求出AD=$\frac{5\sqrt{3}}{3}$.根据等腰三角形三线合一的性质得出BD=$\frac{1}{2}$BC=5,∠BAC=2∠BAD.解Rt△ABD,求出tan∠BAD=$\frac{BD}{AD}$=$\frac{5}{\frac{5\sqrt{3}}{3}}$=$\sqrt{3}$,根据特殊角的三角函数值得到∠BAD=60°,于是∠BAC=120°.
解答 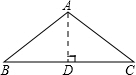 解:如图,作等腰△ABC底边上的高AD.
解:如图,作等腰△ABC底边上的高AD.
∵$\frac{1}{2}$×10AD=$\frac{25}{3}\sqrt{3}$,
∴AD=$\frac{5\sqrt{3}}{3}$.
∵AB=AC,AD⊥BC,
∴BD=$\frac{1}{2}$BC=5,∠BAC=2∠BAD.
在Rt△ABD中,∵∠ADB=90°,
∴tan∠BAD=$\frac{BD}{AD}$=$\frac{5}{\frac{5\sqrt{3}}{3}}$=$\sqrt{3}$,
∴∠BAD=60°,
∴∠BAC=120°.
故答案为120°.
点评 本题考查了解直角三角形,三角形的面积,等腰三角形的性质,特殊角的三角函数值,根据正切函数的定义求出tan∠BAD=$\sqrt{3}$是解题的关键.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
9.某假日,小磊和其他六名同学轻装徒步去郊游.途中,他用18元钱买饮料为大家解渴.每人至少要分得一瓶饮料,商店只有冰红茶和矿泉水,冰红茶3元一瓶,矿泉水2元一瓶,如果18元钱刚好用完则选择购买的方案有( )
| A. | 1种 | B. | 2种 | C. | 3种 | D. | 4种 |
11.不等式组$\left\{\begin{array}{l}{x-2<0}\\{x+5≤3x+7}\end{array}\right.$的整数解有( )
| A. | 0,1,2 | B. | 0,1 | C. | -1,-1 | D. | -1,0,1 |
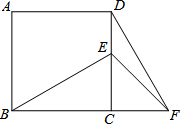 已知:如图,在正方形ABCD中,E为CD边上的一点,F为BC的延长线上一点,CE=CF.
已知:如图,在正方形ABCD中,E为CD边上的一点,F为BC的延长线上一点,CE=CF.