题目内容
6.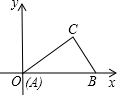 如图,Rt△ABC中,∠C=90°,AB=10,AC=8,Rt△ABC的斜边在x轴的正半轴上,点A与原点重合.随着顶点A由O点出发沿y轴的正半轴方向滑动,点B也沿着x轴向点O滑动,直到与点O重合时运动结束.在这个运动过程中.
如图,Rt△ABC中,∠C=90°,AB=10,AC=8,Rt△ABC的斜边在x轴的正半轴上,点A与原点重合.随着顶点A由O点出发沿y轴的正半轴方向滑动,点B也沿着x轴向点O滑动,直到与点O重合时运动结束.在这个运动过程中.(1)AB中点P经过的路径长$\frac{5}{2}$π.
(2)点C运动的路径长是6.
分析 (1)根据直角三角形斜边中线等于斜边一半,确定中点P的运动路径:以O为圆心,以OP为半径的$\frac{1}{4}$圆弧,半径OP=$\frac{1}{2}$AB=5,代入周长公式计算即可;
(2)分为两种情况:
①当A从O到现在的点A处时,如图2,此时C′A⊥y轴,点C运动的路径长是CC′的长;
②当A再继续向上移动,直到点B与O重合时,如图3,此时点C运动的路径是从C′到C,长是CC′;
分别计算并相加.
解答 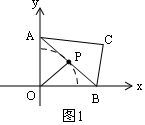 解:(1)如图1,∵∠AOB=90°,P为AB的中点,
解:(1)如图1,∵∠AOB=90°,P为AB的中点,
∴OP=$\frac{1}{2}$AB,
∵AB=10,
∴OP=5,
∴AB中点P运动的轨迹是以O为圆心,以OP为半径的$\frac{1}{4}$圆弧,
即AB中点P经过的路径长=$\frac{1}{4}$×2×5π=$\frac{5}{2}$π;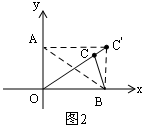
(2)①当A从O到现在的点A处时,如图2,此时C′A⊥y轴,
点C运动的路径长是CC′的长,
∴AC′=OC=8,
∵AC′∥OB,
∴∠AC′O=∠COB,
∴cos∠AC′O=cos∠COB=$\frac{OC}{OB}=\frac{AC′}{OC′}$,
∴$\frac{8}{10}=\frac{8}{OC′}$,
∴OC′=10,
∴CC′=10-8=2;
②当A再继续向上移动,直到点B与O重合时,如图3,
此时点C运动的路径是从C′到C,长是CC′,
CC′=OC′-BC=10-6=4,
综上所述,点C运动的路径长是:4+2=6;
故答案为:(1)$\frac{5}{2}π$; (2)6.
点评 本题考查轨迹问题、直角三角形等知识,解题的关键是学会利用特殊位置解决问题,有难度,并利用了数形结合的思想.

练习册系列答案
相关题目
14.已知等腰三角形的两边长为4,5,则它的周长为( )
| A. | 13 | B. | 14 | C. | 15 | D. | 13或14 |
1.下列命题中是真命题的是( )
| A. | 等腰三角形的对称轴是顶角平分线 | |
| B. | 等边对等角 | |
| C. | 三线合一是指等腰三角形的中线、高线、角平分线重合 | |
| D. | 等腰三角形有1条或3条对称轴 |
11.下列计算结果错误的是( )
| A. | (3ab)3=27a3b3 | B. | 2m6÷(8m3)=0.25m3 | C. | 0.254×28=1 | D. | (2m•2n)ρ=2mnρ |
18.x取任意实数,多项式2x-x2-2的值必定是( )
| A. | 正实数 | B. | 负实数 | C. | 非正实数 | D. | 非负实数 |
 如图是2002年8月在北京召开的国际数学家大会的会标,它取材于我国古代数学家赵爽的《勾股圆方图》,由四个全等的直角三角形和一个小正方形的拼成的大正方形,如果大正方形的面积是5,小正方形的面积是1,直角三角形的较短边为a,较长边为b,那么(a+b)2的值是( )
如图是2002年8月在北京召开的国际数学家大会的会标,它取材于我国古代数学家赵爽的《勾股圆方图》,由四个全等的直角三角形和一个小正方形的拼成的大正方形,如果大正方形的面积是5,小正方形的面积是1,直角三角形的较短边为a,较长边为b,那么(a+b)2的值是( )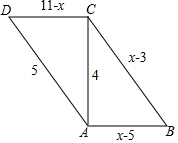 如图,在四边形ABCD中,AB=x-5,CD=11-x,AD=5,BC=x-3,对角线AC=4,AC⊥AB,求证:四边形ABCD是平行四边形.
如图,在四边形ABCD中,AB=x-5,CD=11-x,AD=5,BC=x-3,对角线AC=4,AC⊥AB,求证:四边形ABCD是平行四边形.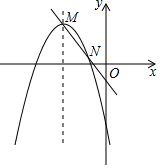 如图,已知抛物线y=-x2+px+q的对称轴为x=-3,过其顶点M的一条直线y=kx+b与该抛物线的另一个交点为N(-1,1).要在坐标轴上找一点P,使得△PMN的周长最小,则点P的坐标为(0,2).
如图,已知抛物线y=-x2+px+q的对称轴为x=-3,过其顶点M的一条直线y=kx+b与该抛物线的另一个交点为N(-1,1).要在坐标轴上找一点P,使得△PMN的周长最小,则点P的坐标为(0,2).