题目内容
16. 如图是2002年8月在北京召开的国际数学家大会的会标,它取材于我国古代数学家赵爽的《勾股圆方图》,由四个全等的直角三角形和一个小正方形的拼成的大正方形,如果大正方形的面积是5,小正方形的面积是1,直角三角形的较短边为a,较长边为b,那么(a+b)2的值是( )
如图是2002年8月在北京召开的国际数学家大会的会标,它取材于我国古代数学家赵爽的《勾股圆方图》,由四个全等的直角三角形和一个小正方形的拼成的大正方形,如果大正方形的面积是5,小正方形的面积是1,直角三角形的较短边为a,较长边为b,那么(a+b)2的值是( )| A. | 4 | B. | 9 | C. | 16 | D. | 25 |
分析 根据大正方形的面积即可求得c2,利用勾股定理可以得到a2+b2=c2,然后求得直角三角形的面积即可求得ab的值,根据(a+b)2=a2+b2+2ab=c2+2ab即可求解.
解答 解:∵大正方形的面积是5,
∴c2=5,
∴a2+b2=c2=5,
∵直角三角形的面积是$\frac{5-1}{4}$=1,
又∵直角三角形的面积是$\frac{1}{2}$ab=1,
∴ab=2,
∴(a+b)2=a2+b2+2ab=c2+2ab=5+2×2=5+4=9.
故选:B.
点评 本题考查了勾股定理以及完全平方公式,正确表示出直角三角形的面积是解题的关键.

练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
6. 如图,在四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定四边形ABCD为平行四边形的是( )
如图,在四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定四边形ABCD为平行四边形的是( )
 如图,在四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定四边形ABCD为平行四边形的是( )
如图,在四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定四边形ABCD为平行四边形的是( )| A. | AB∥CD,AD∥BC | B. | OA=OC,OB=OD | C. | AB=CD,AD∥BC | D. | AB=CD,AD=BC |
7.下列说法正确的是( )
| A. | 0不是单项式 | B. | x没有系数 | C. | x2+$\frac{1}{x}$是多项式 | D. | -$\frac{3xy}{2}$是单项式 |
4.若a>b,则下列各式正确的是( )
| A. | a+4<b+4 | B. | 2a<2b | C. | -5a<-5b | D. | $\frac{a}{3}$-1<$\frac{b}{3}$-1 |
11.数a,b,c在数轴上对应的点的位置如图所示,化简-|a|+|b-c|-|a-b|( )


| A. | -2b+c | B. | 2a+c | C. | 2a-2b+c | D. | -2a+c |
1.下列各数2π,-5,0.$\stackrel{•}{4}$,-3.14,0中,负数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |




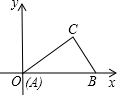 如图,Rt△ABC中,∠C=90°,AB=10,AC=8,Rt△ABC的斜边在x轴的正半轴上,点A与原点重合.随着顶点A由O点出发沿y轴的正半轴方向滑动,点B也沿着x轴向点O滑动,直到与点O重合时运动结束.在这个运动过程中.
如图,Rt△ABC中,∠C=90°,AB=10,AC=8,Rt△ABC的斜边在x轴的正半轴上,点A与原点重合.随着顶点A由O点出发沿y轴的正半轴方向滑动,点B也沿着x轴向点O滑动,直到与点O重合时运动结束.在这个运动过程中.