题目内容
2.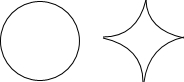 如图,将一个半径为2的圆等分成四段弧,再将这四段弧围成星形,则该图形的面积与原来圆的面积之比为( )
如图,将一个半径为2的圆等分成四段弧,再将这四段弧围成星形,则该图形的面积与原来圆的面积之比为( )| A. | $\frac{4-π}{π}$ | B. | $\frac{{\sqrt{2}}}{π}$ | C. | $\frac{π-1}{π}$ | D. | $\frac{3}{π}$ |
分析 如图,根据圆的面积公式得到半径为2的圆的面积;星形的面积=边长2+2=4的正方形面积-半径为2的圆的面积;再求出两者的比即可求解.
解答  解:2+2=4
解:2+2=4
圆的面积=π×22=4π,
星形的面积=4×4-4π=16-4π,
该图形的面积与原来圆的面积之比为(16-4π):4π=$\frac{4-π}{π}$.
故选:A.
点评 考查了扇形面积的计算,关键是理解星形的面积=边长2+2=4的正方形面积-半径为2的圆的面积.

练习册系列答案
相关题目
13.如果两个角的一边在同一直线上,而另一边互相平行,那么这两个角( )
| A. | 相等 | B. | 互补 | C. | 相等且互余 | D. | 相等或互补 |
10.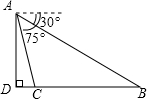 如图,从白塔山山顶A外测得正前方的长江两岸B、C的俯角分别为30°,75°,白塔山的高度AD是600m,则长江的宽度BC等于( )
如图,从白塔山山顶A外测得正前方的长江两岸B、C的俯角分别为30°,75°,白塔山的高度AD是600m,则长江的宽度BC等于( )
 如图,从白塔山山顶A外测得正前方的长江两岸B、C的俯角分别为30°,75°,白塔山的高度AD是600m,则长江的宽度BC等于( )
如图,从白塔山山顶A外测得正前方的长江两岸B、C的俯角分别为30°,75°,白塔山的高度AD是600m,则长江的宽度BC等于( )| A. | 300($\sqrt{3}$+1)m | B. | 1200($\sqrt{3}$-1)m | C. | 1800($\sqrt{3}$-1)m | D. | 2400($\sqrt{2}$-1)m |
7.为了说明命题“当b<0时,关于x的一元二次方程x2+bx+2=0必有实数解”是假命题,可以举的一个反例是( )
| A. | b=2 | B. | b=3 | C. | b=-2 | D. | b=-3 |
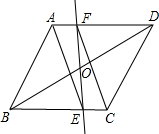 如图,在?ABCD中,O是对角线BD的中点,过O点的一条直线分别与BC相交于E,与AD相交于F,求证:四边形AECF是平行四边形.
如图,在?ABCD中,O是对角线BD的中点,过O点的一条直线分别与BC相交于E,与AD相交于F,求证:四边形AECF是平行四边形.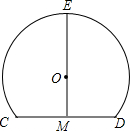 一个隧道的横截面如图所示,它的形状是以点O为圆心,5为半径的圆的一部分,M是⊙O中弦CD的中点,EM经过圆心O交⊙O于点E.若CD=6,则隧道的高(ME的长)为( )
一个隧道的横截面如图所示,它的形状是以点O为圆心,5为半径的圆的一部分,M是⊙O中弦CD的中点,EM经过圆心O交⊙O于点E.若CD=6,则隧道的高(ME的长)为( )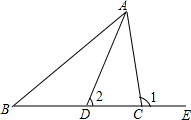 如图,AD是△ABC的角平分线,点E在BC的延长线上,求证:∠B+∠1=2∠2.
如图,AD是△ABC的角平分线,点E在BC的延长线上,求证:∠B+∠1=2∠2.