题目内容
14.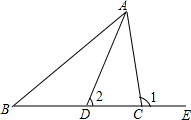 如图,AD是△ABC的角平分线,点E在BC的延长线上,求证:∠B+∠1=2∠2.
如图,AD是△ABC的角平分线,点E在BC的延长线上,求证:∠B+∠1=2∠2.
分析 根据三角形的外角性质得出∠1=∠B+∠BAC,∠2=∠B+∠BAD,再利用角平分线的定义转化证明即可.
解答 证明:∵∠1=∠B+∠BAC,∠2=∠B+∠BAD,
∵AD是△ABC的角平分线,
∴∠BAC=2∠BAD,
∴∠B+∠1=∠B+∠B+∠BAC=2∠B+2∠BAD=2∠2.
点评 此题考查三角形外角的性质,关键是根据三角形的外角性质得出∠1=∠B+∠BAC,∠2=∠B+∠BAD.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.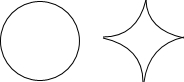 如图,将一个半径为2的圆等分成四段弧,再将这四段弧围成星形,则该图形的面积与原来圆的面积之比为( )
如图,将一个半径为2的圆等分成四段弧,再将这四段弧围成星形,则该图形的面积与原来圆的面积之比为( )
 如图,将一个半径为2的圆等分成四段弧,再将这四段弧围成星形,则该图形的面积与原来圆的面积之比为( )
如图,将一个半径为2的圆等分成四段弧,再将这四段弧围成星形,则该图形的面积与原来圆的面积之比为( )| A. | $\frac{4-π}{π}$ | B. | $\frac{{\sqrt{2}}}{π}$ | C. | $\frac{π-1}{π}$ | D. | $\frac{3}{π}$ |
 如图,直线a∥b,∠1=50°,∠2=30°,则∠3=20°.
如图,直线a∥b,∠1=50°,∠2=30°,则∠3=20°.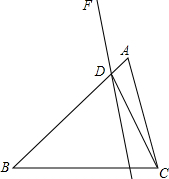 如图,已知△ABC,D为AB边上一点,∠BDC=∠ACB,过点D作直线DF.
如图,已知△ABC,D为AB边上一点,∠BDC=∠ACB,过点D作直线DF.