题目内容
13.如果两个角的一边在同一直线上,而另一边互相平行,那么这两个角( )| A. | 相等 | B. | 互补 | C. | 相等且互余 | D. | 相等或互补 |
分析 首先根据题意作图,然后根据两直线平行,同位角相等与邻补角的关系,即可求得答案.
解答 解:如图,分两种情况:
①∠A与∠1的一边在直线AC上,另一边AB∥DE,
∴∠1=∠A;
②∠A与∠2的一边在直线AC上,另一边AB∥DF,
∵∠1+∠2=180°,∠1=∠A,
∴∠2+∠A=180°.
综上,可知这两个角的关系是相等或互补.
故选D.
点评 此题考查了平行线的性质与邻补角的定义,注意两直线平行,同位角相等定理的应用.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
1.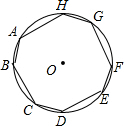 如图,已知在⊙O中,AB=CD=EF=HG,BC=DE=FG=AH,则∠AHG的度数是( )
如图,已知在⊙O中,AB=CD=EF=HG,BC=DE=FG=AH,则∠AHG的度数是( )
 如图,已知在⊙O中,AB=CD=EF=HG,BC=DE=FG=AH,则∠AHG的度数是( )
如图,已知在⊙O中,AB=CD=EF=HG,BC=DE=FG=AH,则∠AHG的度数是( )| A. | 120° | B. | 125° | C. | 130° | D. | 135° |
2.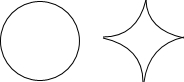 如图,将一个半径为2的圆等分成四段弧,再将这四段弧围成星形,则该图形的面积与原来圆的面积之比为( )
如图,将一个半径为2的圆等分成四段弧,再将这四段弧围成星形,则该图形的面积与原来圆的面积之比为( )
 如图,将一个半径为2的圆等分成四段弧,再将这四段弧围成星形,则该图形的面积与原来圆的面积之比为( )
如图,将一个半径为2的圆等分成四段弧,再将这四段弧围成星形,则该图形的面积与原来圆的面积之比为( )| A. | $\frac{4-π}{π}$ | B. | $\frac{{\sqrt{2}}}{π}$ | C. | $\frac{π-1}{π}$ | D. | $\frac{3}{π}$ |
 如图,直线a∥b,∠1=50°,∠2=30°,则∠3=20°.
如图,直线a∥b,∠1=50°,∠2=30°,则∠3=20°.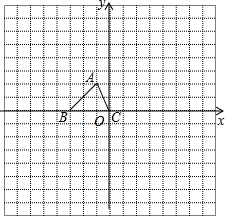 如图,已知△ABC的三个顶点的坐标分别为A(-1,2)、B(-3,0)、C(0,0).
如图,已知△ABC的三个顶点的坐标分别为A(-1,2)、B(-3,0)、C(0,0).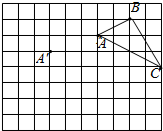 在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示,现将△ABC平移,使点A变换为点A′,点B′、C′分别是B、C的对应点.
在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示,现将△ABC平移,使点A变换为点A′,点B′、C′分别是B、C的对应点.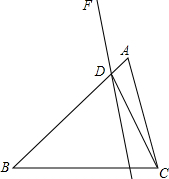 如图,已知△ABC,D为AB边上一点,∠BDC=∠ACB,过点D作直线DF.
如图,已知△ABC,D为AB边上一点,∠BDC=∠ACB,过点D作直线DF.