题目内容
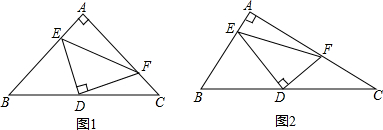
 如图,把等边三角形ABD和等边三角形BCD拼合在一起,E在AB边上移动,且满足AE=BF,试说明不论E怎样移动,△EDF总是等边三角形.
如图,把等边三角形ABD和等边三角形BCD拼合在一起,E在AB边上移动,且满足AE=BF,试说明不论E怎样移动,△EDF总是等边三角形.考点:全等三角形的判定与性质,等边三角形的判定与性质
专题:证明题
分析:根据等边三角形性质得出BD=AD,∠CBD=∠A=60°,∠ADB=60°,根据SAS推出△EAD≌△FBD,推出DE=DF,∠ADE=∠BDF,求出∠EDF=60°,根据等边三角形的判定推出即可.
解答:解:∵△ABD和△BCD是等边三角形,
∴BD=AD,∠CBD=∠A=60°,∠ADB=60°,
在△EAD和△FBD中
,
∴△EAD≌△FBD,
∴DE=DF,∠ADE=∠BDF,
∴∠EDF=∠BDF+∠BDE=∠ADE+∠BDE=∠ADB=60°,
∵DE=DF,
∴△EDF是等边三角形.
∴BD=AD,∠CBD=∠A=60°,∠ADB=60°,
在△EAD和△FBD中
|
∴△EAD≌△FBD,
∴DE=DF,∠ADE=∠BDF,
∴∠EDF=∠BDF+∠BDE=∠ADE+∠BDE=∠ADB=60°,
∵DE=DF,
∴△EDF是等边三角形.
点评:本题考查了全等三角形的性质和判定,等边三角形的性质和判定的应用,注意:有一个角等于60度的等腰三角形是等边三角形.

练习册系列答案
相关题目
下列方程是一元二次方程的是( )
①2x2+x=10;②2x2-3xy+4=0;③x2-
=1;④x2-
+2=0;⑤x2=0.
①2x2+x=10;②2x2-3xy+4=0;③x2-
| 1 |
| x |
| x |
| 2 |
| A、①② | B、①②④⑤ |
| C、①③④ | D、①④⑤ |
 在直径为26cm的圆柱形油槽内装入一些油后,截面如图所示,若油面宽AB=24cm,则油的最大深度为
在直径为26cm的圆柱形油槽内装入一些油后,截面如图所示,若油面宽AB=24cm,则油的最大深度为