题目内容
 在直径为26cm的圆柱形油槽内装入一些油后,截面如图所示,若油面宽AB=24cm,则油的最大深度为
在直径为26cm的圆柱形油槽内装入一些油后,截面如图所示,若油面宽AB=24cm,则油的最大深度为考点:垂径定理的应用,勾股定理
专题:
分析:连接OB,过点O作OC⊥AB于点D,交⊙O于点C,先由垂径定理求出BD的长,再根据勾股定理求出OD的长,进而可得出CD的长.
解答: 解:连接OB,过点O作OC⊥AB于点D,交⊙O于点C,
解:连接OB,过点O作OC⊥AB于点D,交⊙O于点C,
∵AB=24cm,
∴BD=
AB=
×24=12cm,
∵⊙O的直径为26cm,
∴OB=OC=12cm,
在Rt△OBD中,OD=
=
=5cm,
∴CD=OC-OD=13-5=8cm.
故答案为:8.
 解:连接OB,过点O作OC⊥AB于点D,交⊙O于点C,
解:连接OB,过点O作OC⊥AB于点D,交⊙O于点C,∵AB=24cm,
∴BD=
| 1 |
| 2 |
| 1 |
| 2 |
∵⊙O的直径为26cm,
∴OB=OC=12cm,
在Rt△OBD中,OD=
| OB2-BD2 |
| 132-122 |
∴CD=OC-OD=13-5=8cm.
故答案为:8.
点评:本题考查的是垂径定理的应用,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
相关题目
在同一平面直角坐标系中,函数y=
与函数y=-x的图象交点个数是( )
| 1 |
| x |
| A、0个 | B、1个 | C、2个 | D、3个 |
如果零上5℃记作+5℃,那么零下10℃记作( )
| A、-5 | B、-10 |
| C、-10℃ | D、-5℃ |
 已知抛物线y1=ax2+bx+c(a≠0)的顶点坐标是(1,4),它与直线y2=x+1的一个交点的横坐标为2.
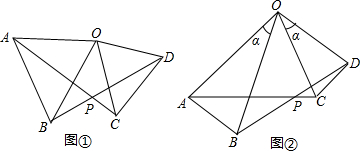
已知抛物线y1=ax2+bx+c(a≠0)的顶点坐标是(1,4),它与直线y2=x+1的一个交点的横坐标为2. 如图,把等边三角形ABD和等边三角形BCD拼合在一起,E在AB边上移动,且满足AE=BF,试说明不论E怎样移动,△EDF总是等边三角形.
如图,把等边三角形ABD和等边三角形BCD拼合在一起,E在AB边上移动,且满足AE=BF,试说明不论E怎样移动,△EDF总是等边三角形. 如图,在△ABC中,点D是BC上一点,∠BAD=78°,AB=AD=DC,则∠C=
如图,在△ABC中,点D是BC上一点,∠BAD=78°,AB=AD=DC,则∠C= 如图,正五边形的一个外角∠1=
如图,正五边形的一个外角∠1=