题目内容
20.如图,已知以AE为直径的半圆圆心为O,半径为5,矩形ABCD的顶点B在直径AE上,顶点C在半圆上,AB=8,点P为半圆上一点.(1)矩形ABCD的边BC的长为4;
(2)将矩形沿直线AP折叠,点B落在点B′.
①点B′到直线AE的最大距离是8;
②当点P与点C重合时,如图所示,AB′交DC于点M.
求证:四边形AOCM是菱形,并通过证明判断CB′与半圆的位置关系;
③当EB′∥BD时,直接写出EB′的长.

分析 (1)如图1中,在Rt△OBC中,求出BC即可.
(2)①如图1中,当点B′在直线AD上时,点B'到 AE的距离最大,最大距离为8.
②首先证明四边形AOCM是平行四边形,由OA=OC即可判定四边形AOCM是菱形.只要证明∠OCB′=90°即可判定CB′与半圆相切.
③如图3中,当EB′∥BD时,作AF⊥EB′于F.由△AEF∽△DBA,可得$\frac{EF}{AB}$=$\frac{AE}{BD}$=$\frac{AF}{AD}$,推出EF=4$\sqrt{5}$,AF=2$\sqrt{5}$,在Rt△AFB′中,FB′=$\sqrt{AB{′}^{2}+A{F}^{2}}$=2$\sqrt{11}$,即可推出EB′=4$\sqrt{5}$+2$\sqrt{11}$.如图4中,当EB′∥BD时,作AF⊥EB′于F,同法可求EB′.
解答 解:(1)如图1中,连接OC.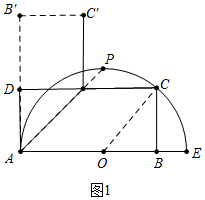
在Rt△BOC中,∵∠OBC=90°,OC=5,OB=3,
∴BC=$\sqrt{O{C}^{2}-O{B}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4,
故答案为4.
(2)①如图1中,当点B′在直线AD上时,点B'到 AE的距离最大,最大距离为8.
故答案为8.
②证明:如图2中,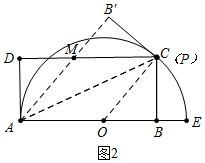
由折叠可知:∠OAC=∠MAC.
∵OA=OC,
∴∠OAC=∠OCA.
∴∠OCA=∠MAC.
∴OC∥AM.
又∵CM∥OA,
∴四边形AOCM是平行四边形.
又∵OA=OC,
∴□AOCM是菱形.
结论:CB′与半圆相切.
理由:由折叠可知:∠ABˊC=∠ABC=90°.
∵OC∥AM
∴∠ABˊC+∠BˊCO=180°.
∴∠BˊCO=90°.
∴CBˊ⊥OC.
∴CBˊ与半圆相切.
③如图3中,当EB′∥BD时,作AF⊥EB′于F.
由△AEF∽△DBA,
∴$\frac{EF}{AB}$=$\frac{AE}{BD}$=$\frac{AF}{AD}$,
∴EF=4$\sqrt{5}$,AF=2$\sqrt{5}$,
在Rt△AFB′中,FB′=$\sqrt{AB{′}^{2}+A{F}^{2}}$=2$\sqrt{11}$,
∴EB′=4$\sqrt{5}$+2$\sqrt{11}$.
如图4中,当EB′∥BD时,作AF⊥EB′于F,
同法可得EF=4$\sqrt{5}$,FB′=2$\sqrt{11}$,
∴EB′=4$\sqrt{5}$-2$\sqrt{11}$.
综上所述,满足条件的EB′的长为4$\sqrt{5}$+2$\sqrt{11}$或4$\sqrt{5}$-2$\sqrt{11}$.
点评 本题考查圆综合题、矩形的性质、翻折变换、平行四边形的判定和性质、勾股定理、解直角三角形等知识,解题的关键是学会用分类讨论的思想思考问题,学会添加常用辅助线,构造直角三角形解决问题,属于中考压轴题.

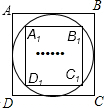 如图,我们把先作正方形ABCD的内切圆,再作这个内切圆的内接正方形A1B1C1D1.称为第一次数学操作,解下列,作正方形A1B1C1D1的内切圆,再作这个内切圆的内接正方形A2B2C2D2,称为第二次数学操作,按此规律如此下去,…,当完成第n次数学操作后,得到正方形AnBnCnDn,则$\frac{{A}_{n}{B}_{n}}{AB}$的值为( )
如图,我们把先作正方形ABCD的内切圆,再作这个内切圆的内接正方形A1B1C1D1.称为第一次数学操作,解下列,作正方形A1B1C1D1的内切圆,再作这个内切圆的内接正方形A2B2C2D2,称为第二次数学操作,按此规律如此下去,…,当完成第n次数学操作后,得到正方形AnBnCnDn,则$\frac{{A}_{n}{B}_{n}}{AB}$的值为( )| A. | ($\frac{\sqrt{2}}{2}$)n | B. | ($\frac{1}{2}$)n | C. | ($\frac{\sqrt{3}}{2}$)n | D. | ($\frac{3}{4}$)n |
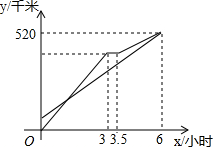 甲、乙两车从A地出发沿同一路线驶向B地,甲车匀速驶向B地,甲车出发30分钟后,乙车才出发,乙先匀速行驶一段时间后,到达货站装货后继续行驶,速度减少了56千米/时,结果与甲车同时到达B地,甲乙两车距A地的路程y(千米)与乙车行驶时间x(时)之间的函数图象如图所示,下列说法中正确的是( )
甲、乙两车从A地出发沿同一路线驶向B地,甲车匀速驶向B地,甲车出发30分钟后,乙车才出发,乙先匀速行驶一段时间后,到达货站装货后继续行驶,速度减少了56千米/时,结果与甲车同时到达B地,甲乙两车距A地的路程y(千米)与乙车行驶时间x(时)之间的函数图象如图所示,下列说法中正确的是( )| A. | 甲车从A地到B地行驶了6小时 | |
| B. | 甲的速度是120千米/时 | |
| C. | 乙出发90分钟追上甲 | |
| D. | 当两车在行驶过程中,相距40千米时,x=2或3.5 |
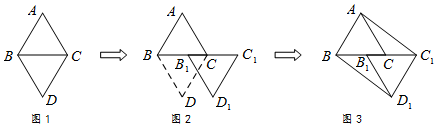
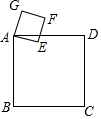 如图,已知正方形ABCD与正方形AEFG的边长分别为4cm,1cm,若将正方形AEFG绕点A旋转,则在旋转过程中,点C、F之间的最小距离为3$\sqrt{2}$cm.
如图,已知正方形ABCD与正方形AEFG的边长分别为4cm,1cm,若将正方形AEFG绕点A旋转,则在旋转过程中,点C、F之间的最小距离为3$\sqrt{2}$cm. 如图,在△ABC中,∠A=64°,∠ABC与∠ACD的平分线交于点A1,则∠A1=32°;∠A1BC与∠A1CD的平分线相交于点A2,得∠A2;…;∠An-1BC与∠An-1CD的平分线相交于点An,要使∠An的度数为整数,则n的值最大为6.
如图,在△ABC中,∠A=64°,∠ABC与∠ACD的平分线交于点A1,则∠A1=32°;∠A1BC与∠A1CD的平分线相交于点A2,得∠A2;…;∠An-1BC与∠An-1CD的平分线相交于点An,要使∠An的度数为整数,则n的值最大为6.