题目内容
11.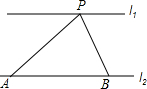 如图,直线l1∥l2,两直线之间的距离为2,A,B是直线l2上两点,AB=4,点P直线l1上一个动点,则∠APB的最大值为90°.
如图,直线l1∥l2,两直线之间的距离为2,A,B是直线l2上两点,AB=4,点P直线l1上一个动点,则∠APB的最大值为90°.
分析 结合已知条件作图如下“以线段AB为直径作圆,圆与直线l1交于点P,在l1上任找一点P′(与点P不重合),连接AP′交圆于点C,连接BC”,根据线段AB为直径可得出∠APB=∠ACB=90°,再结合三角形外角的性质即可得出∠APB>∠AP′B,由此即可得出结论.
解答 解:∵AB=4,直线l1∥l2,两直线之间的距离为2,
∴以线段AB为直径作圆,圆与直线l1交于点P,在l1上任找一点P′(与点P不重合),连接AP′交圆于点C,连接BC,如图所示.
∵线段AB为直径,
∴∠APB=∠ACB=90°,
∵∠ACB=∠AP′B+∠CBP′,
∴∠APB=∠ACB>∠AP′B.
∴当点P在线段AB的垂直平分线上时,∠APB最大,最大值为90°.
故答案为:90°.
点评 本题考查了圆周角以及三角形外角的性质,解题的关键是找出∠APB>∠AP′B.本题属于中档题,难度不大,但方法不大好找,此处巧妙的借助了作圆,利用圆周角相等,再根据三角形的外角的性质找出结论.

练习册系列答案
相关题目
1.下列各式中,一定是二次根式的是( )
| A. | $\sqrt{-2017}$ | B. | $\root{3}{x}$ | C. | $\sqrt{{x}^{2}+1}$ | D. | $\sqrt{x+2016}$ |
2.方程(x-2)(x+3)-(x-2)(2x-1)=0的解是( )
| A. | x=2 | B. | x=4 | C. | x=2或x=4 | D. | x=2或x=-3或x=$\frac{1}{2}$ |
6.下列计算正确的是( )
| A. | $\sqrt{3}$-$\sqrt{2}$=1 | B. | $\sqrt{3}×\sqrt{6}=3\sqrt{2}$ | C. | $\sqrt{2}+\sqrt{3}=\sqrt{5}$ | D. | (2$\sqrt{3}$)2=6 |
16.下列两个三角形中,一定全等的是( )
| A. | 有一个角是40°,腰相等的两个等腰三角形 | |
| B. | 有一个角是100°,底相等的两个等腰三角形 | |
| C. | 两个等边三角形 | |
| D. | 有一条边相等,有一个内角相等的两个等腰三角形 |
20.下列运算中正确的是( )
| A. | 2x+3y=5xy | B. | a3-a2=a | C. | (a-1)(a-2)=a2+a-2 | D. | (a-ab)÷a=1-b |
1.下列运算中,错误的是( )
| A. | 2a-3a=-a | B. | (-ab)3=-a3b3 | C. | a6÷a2=a4 | D. | a•a2=a2 |
