题目内容

2．方程（x-2）（x+3）-（x-2）（2x-1）=0的解是（　　）
A．x=2B．x=4C．x=2或x=4D．x=2或x=-3或x=$\frac{1}{2}$

分析 将方程左边因式分解可得（x-2）（-x+4）=0，继而可得x-2=0或-x+4=0，解方程得x的值．

解答 解：左边因式分解可得，（x-2）[（x+3）-（2x-1）]=0，
整理，得：（x-2）（-x+4）=0，
∴x-2=0或-x+4=0，
解得：x=2或x=4，
故选：C．

点评 此题考查了一元二次方程的解法；只有当方程的一边能够分解成两个一次因式，而另一边是0的时候，才能应用因式分解法解一元二次方程．分解因式时，要根据情况灵活运用学过的因式分解的几种方法．

练习册系列答案
相关题目
12．等腰△ABC中，AB=AC，以AB为直径作圆交BC于点D，请仅用无刻度的直尺，根据下列条件分别在图1、图2中画一条弦，使这条弦的长度等于弦BD．（保留作图痕迹，不写作法）
（1）如图1，∠A＜90°；
（2）如图2，∠A＞90°．
13．下列各式表示正确的是（　　）
A．$\sqrt{25}=±5$B．$±\sqrt{25}=5$C．$\root{3}{-27}$=-3D．$±\sqrt{（-5）^{2}}=-5$
10．下列各组数是方程组$\left\{\begin{array}{l}{x+y=5}\\{2x-y=1}\end{array}\right.$的解的是（　　）
A．$\left\{\begin{array}{l}{x=2}\\{y=3}\end{array}\right.$B．$\left\{\begin{array}{l}{x=1}\\{y=4}\end{array}\right.$C．$\left\{\begin{array}{l}{x=3}\\{y=2}\end{array}\right.$D．$\left\{\begin{array}{l}{x=4}\\{y=1}\end{array}\right.$
17．阅读下面材料：
在数学课上，老师提出如下问题：

小敏的作法如下：

老师说：“小敏的作法正确．”
请回答：小敏的作图依据是对角线互相平分的四边形是平行四边形；有一个角是直角的平行四边形是矩形．
7．下列运算正确的是（　　）
A．-$\sqrt{-25}$=5B．$\root{3}{1{0}^{6}}$=102C．$\sqrt{4+\frac{9}{16}}$=2$\frac{3}{4}$D．$\sqrt{0.25}$=±0.5
14．下列命题中，正确的是（　　）
A．菱形的对角线互相垂直且平分B．平行四边形的对角线相等
C．矩形的对角线互相垂直D．梯形的对角线相等
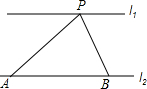11．如图，直线l1∥l2，两直线之间的距离为2，A，B是直线l2上两点，AB=4，点P直线l1上一个动点，则∠APB的最大值为90°．
12．下列运算正确的是（　　）
A．a2+a2=a4B．a6÷a3=a2C．（a3b）2=a5b3D．a3×a2=a5

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网