题目内容
1．下列各式中，一定是二次根式的是（ ）| A． | $\sqrt{-2017}$ | B． | $\root{3}{x}$ | C． | $\sqrt{{x}^{2}+1}$ | D． | $\sqrt{x+2016}$ |
分析 根据二次根式的性质：二次根式中的被开方数必须是非负数，否则二次根式无意义，逐一判断．
解答 解：A、被开方数为负数，二次根式无意义，故选项错误；
B、是三次根式，故选项错误；
C、x2+1＞0一定成立，被开方数是非负数，故选项正确；
D、当x＜-2016时，二次根式无意义，故选项错误．
故选C．
点评 主要考查了二次根式的意义和性质．
概念：式子$\sqrt{a}$（a≥0）叫二次根式．
性质：二次根式中的被开方数必须是非负数，否则二次根式无意义．
练习册系列答案
暑假衔接培优教材浙江工商大学出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
9．下列各式一定成立的是（ ）
| A． | 2a+3b=5ab | B． | （a-b）2=a2-b2 | C． | （3a3）2=9a6 | D． | a6÷a2=a3 |
16．下列说法中，正确的是（ ）
| A． | $\sqrt{4}$的平方根是±$\sqrt{2}$ | B． | -a2一定没有平方根 | ||
| C． | 0.9的平方根是±0.3 | D． | a2-1一定有平方根 |
6．下列各式中，运算正确的是（ ）
①（22a）2=4a2；
②（-$\frac{1}{3}$x+1）（1+$\frac{1}{3}$x）=1-$\frac{1}{9}$x2；
③（m-1）2（1-m）3=（m-1）5；
④（-a-b）2-a2=2ab+b2．
①（22a）2=4a2；
②（-$\frac{1}{3}$x+1）（1+$\frac{1}{3}$x）=1-$\frac{1}{9}$x2；
③（m-1）2（1-m）3=（m-1）5；
④（-a-b）2-a2=2ab+b2．
| A． | ①② | B． | ②③ | C． | ②④ | D． | ③④ |
13．下列各式表示正确的是（ ）
| A． | $\sqrt{25}=±5$ | B． | $±\sqrt{25}=5$ | C． | $\root{3}{-27}$=-3 | D． | $±\sqrt{（-5）^{2}}=-5$ |
10．下列各组数是方程组$\left\{\begin{array}{l}{x+y=5}\\{2x-y=1}\end{array}\right.$的解的是（ ）
| A． | $\left\{\begin{array}{l}{x=2}\\{y=3}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{x=1}\\{y=4}\end{array}\right.$ | C． | $\left\{\begin{array}{l}{x=3}\\{y=2}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{x=4}\\{y=1}\end{array}\right.$ |
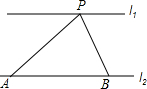如图，直线l1∥l2，两直线之间的距离为2，A，B是直线l2上两点，AB=4，点P直线l1上一个动点，则∠APB的最大值为90°．