题目内容
 已知在平面直角坐标系中,点A,B表示两个大型综合商场,坐标分别为A(2,-5),B(5,1).x轴,y轴分别表示庆春路和延安路,请在同一个坐标系内画出满足下列条件的点(保留画图痕迹),并求出点C的坐标.
已知在平面直角坐标系中,点A,B表示两个大型综合商场,坐标分别为A(2,-5),B(5,1).x轴,y轴分别表示庆春路和延安路,请在同一个坐标系内画出满足下列条件的点(保留画图痕迹),并求出点C的坐标.(1)现打算在延安路上建一个地铁出口站C,使得它到两个商场的直线距离最小;
(2)小敏到庆春路上的书店D买书,它到A商场的距离与它到B商场的直线距离之差达到最大.
考点:一次函数综合题
专题:
分析:(1)线段垂直平分线的性质,可得A点关于y轴的对称点,根据线段的性质,可得线段A′B,根据待定系数法,可得直线A′B的解析式,根据自变量为0,可得答案;
(2)线段垂直平分线的性质,可得B点关于x轴的对称点B′,根据三角形两边之差小于第三边,当A,B′,D三点共线,根据待定系数法,可得直线AB′的解析式,根据函数值为0,可得答案.
(2)线段垂直平分线的性质,可得B点关于x轴的对称点B′,根据三角形两边之差小于第三边,当A,B′,D三点共线,根据待定系数法,可得直线AB′的解析式,根据函数值为0,可得答案.
解答:解: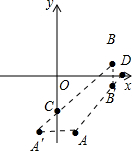
(1)C点如图,
作A关于y轴的对称点A′,连结A′B交y轴于点C
A′点的坐标是(-2,-5),B(5,1)
解得A′B直线解析式:y=-
x-
.
当x=0时,y=-
∴点C的坐标为(0,-
);
(2)D点如图,
作点B关于x轴的对称点B′,连结AB’延长交x轴于D
∵若A,B′,D三点不共线,根据三角形两边之差小于第三条边可得AD-B′D<AB′
∴当A,B′,D三点共线时,AD-B′D=AB′,此时AD-B′D有最大值,最大值为AB′的长度,
此时,点D在直线AB′上,
根据题意由A(2,-5),B′(5,-1)代入可得y=
x-
,
当y=0时,x=
,
∴当AD-BD有最大值时,点D的坐标为(
,0).

(1)C点如图,
作A关于y轴的对称点A′,连结A′B交y轴于点C
A′点的坐标是(-2,-5),B(5,1)
解得A′B直线解析式:y=-
| 6 |
| 7 |
| 23 |
| 7 |
当x=0时,y=-
| 23 |
| 7 |
∴点C的坐标为(0,-
| 23 |
| 7 |
(2)D点如图,
作点B关于x轴的对称点B′,连结AB’延长交x轴于D
∵若A,B′,D三点不共线,根据三角形两边之差小于第三条边可得AD-B′D<AB′
∴当A,B′,D三点共线时,AD-B′D=AB′,此时AD-B′D有最大值,最大值为AB′的长度,
此时,点D在直线AB′上,
根据题意由A(2,-5),B′(5,-1)代入可得y=
| 4 |
| 3 |
| 23 |
| 3 |
当y=0时,x=
| 23 |
| 4 |
∴当AD-BD有最大值时,点D的坐标为(
| 23 |
| 4 |
点评:本题考查了一次函数的综合题,(1)利用了线段垂直平分线的性质,两点之间线段最短,待定系数法求解析式,(2)利用了三角形三边的关系.

练习册系列答案
相关题目
 如图,矩形ABCD中,E为CD的中点,连接AE并延长交BC的延长线于点F,连接BD交AF于H,AD=5
如图,矩形ABCD中,E为CD的中点,连接AE并延长交BC的延长线于点F,连接BD交AF于H,AD=5 如图,菱形ABCD中,点M为AD的中点,点N在AB上,DE⊥BC的延长线于点E,连接BM、DN、EN,∠AND=∠MBC.
如图,菱形ABCD中,点M为AD的中点,点N在AB上,DE⊥BC的延长线于点E,连接BM、DN、EN,∠AND=∠MBC.
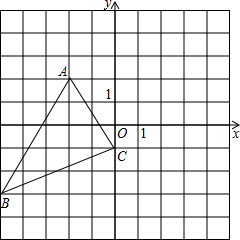 如图,将三角形ABC向右平移5个单位长度,再向上平移3个单位长度请回答下列问题:
如图,将三角形ABC向右平移5个单位长度,再向上平移3个单位长度请回答下列问题: