题目内容
5.已知:如图(1),四边形ABCD为正方形,E为CD边上的一点,连结AE,并以AE为对称轴,作与△ADE成轴对称的图形△AGE,延长EG(或GE)交直线BC于F.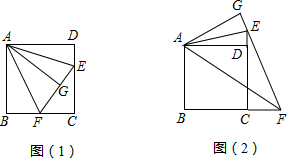
(1)求证:DE+BF=EF;∠EAF=45°;
(2)若E为CD延长线上一点,如图(2),则线段DE,BF,EF之间有怎样的关系,∠EAF等于几度?请说明理由.
分析 (1)由正方形的性质和轴对称,AB=AG,∠ABF=∠AGE,从而判断出△ABF≌△AGF,即可;
(2)同(1)方法即可.
解答 解:(1)∵四边形ABCD是正方形,
∴AD=AB,∠B=∠D,
∵△ADE成轴对称的图形△AGE,
∴AD=AG,DE=GE,∠AGE=∠D=90°,∠GAE=∠DAE,
∴AG=AB,∠AGE=∠AGF=∠D=∠BAD=∠ABF=90°,
在△ABF和△AGF中$\left\{\begin{array}{l}{AB=AG}\\{∠ABF=∠AGE}\\{AF=AF}\end{array}\right.$,
△ABF≌△AGF,
∴BF=GF,∠BAF=∠GAF,
∴DE+BF=GE+GF=EF.
∠EAF=∠GAE+∠GAF=$\frac{1}{2}$∠DAB=45°;
(2)∵四边形ABCD是正方形,
∴AD=AB,∠B=∠D,
∵△ADE成轴对称的图形△AGE,
∴AD=AG,DE=GE,∠AGE=∠ADE=90°,∠GAE=∠DAE,
∴AG=AB,∠AGE=∠BAD=∠ABF=90°,
在△ABF和△AGF中$\left\{\begin{array}{l}{AB=AG}\\{∠ABF=∠AGE}\\{AF=AF}\end{array}\right.$,
∴△ABF≌△AGF,
∴BF=GF,∠BAF=∠GAF,
∴BF=GF=GE+EF=DE+EF;
∵∠BAF+∠DAF=90°,
∴∠GAF+∠DAF=90°,
∵∠GAF=∠EAF+∠GAE,
∴∠EAF+∠GAE+∠DAF=2∠EAF=90°,
∴∠EAF=45°.
点评 此题是正方形的性质,主要考查了正方形的性质,轴对称,全等三角形的性质和判定,解本题的关键是判断出△ABF≌△AGF.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.某商店需要购进甲、乙两种商品共160件,其进价和售价如表:(注:获利=售价-进价)若商店计划销售完这批商品后能获利1100元,问甲、乙两种商品应分别购进多少件?
| 甲 | 乙 | |
| 进价(元/件) | 15 | 35 |
| 售价(元/件) | 20 | 45 |
 如图是由10个相同的小长方形拼成的长方形图案,则每块小长方形的面积为400cm2.
如图是由10个相同的小长方形拼成的长方形图案,则每块小长方形的面积为400cm2. 如图,已知点A、B、C是⊙O上的点,其中点C是弧AB的中点,OC=4cm,点P是OC延长线上一点,连接PA、PB.
如图,已知点A、B、C是⊙O上的点,其中点C是弧AB的中点,OC=4cm,点P是OC延长线上一点,连接PA、PB.