Question

10．在△ABC中，AB=AC，MN垂直平分AB分别交AB、BC于M、N．如果△ACN是等腰三角形，那么∠B的大小是45°或36°．

Answer 1

分析 首先根据线段垂直平分线的性质得出NA=NB，即可得到∠B=∠BAN=∠C．然后对△ANC中的边进行讨论，然后在△ABC中，利用三角形内角和定理即可求得∠B的度数．

解答 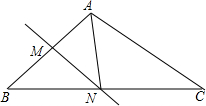解：∵MN是AB的中垂线，
∴NB=NA．
∴∠B=∠BAN，
∵AB=AC，
∴∠B=∠C．
设∠B=x°，则∠C=∠BAN=x°．
1）当AN=NC时，∠CAN=∠C=x°．
则在△ABC中，根据三角形内角和定理可得：4x=180，
解得：x=45，则∠B=45°；
2）当AN=AC时，∠ANC=∠C=x°，而∠ANC=∠B+∠BAN，故此时不成立；
3）当CA=CN时，∠NAC=∠ANC=$\frac{180°-x°}{2}$．
在△ABC中，根据三角形内角和定理得到：x+x+x+$\frac{180-x}{2}$=180，
解得：x=36．
即∠B的度数为45°或36°．
故答案为45°或36°．

点评 本题考查了线段垂直平分线的性质，等腰三角形的性质，三角形内角和定理，正确对△ANC的边进行讨论是解题的关键．