题目内容
14.先化简再求值:$\frac{2}{{m}^{2}-4}$•($\frac{{m}^{2}+4}{4m}$-1)÷($\frac{1}{2}$-$\frac{1}{m}$),其中m是方程x2-x-2=0的根.分析 先把原分式化简再代入解答即可.
解答 解:$\frac{2}{{m}^{2}-4}$•($\frac{{m}^{2}+4}{4m}$-1)÷($\frac{1}{2}$-$\frac{1}{m}$)
=$\frac{2}{(m+2)(m-2)}•\frac{(m-2)^{2}}{4m}•\frac{2m}{m-2}$
=$\frac{1}{m+2}$,
因为m是方程x2-x-2=0的根,
可得:m1=2,m2=-1,
因为m=2原分式无意义,
所以m=-1,
把m=-1代入$\frac{1}{m+2}=1$.
点评 此题考查分式的化简求值,关键是把原分式化简,再利用分式是否有意义进行解答.

练习册系列答案
 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案
相关题目
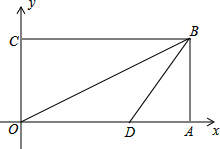 如图,在平面直角坐标系中,点O是坐标原点,四边形OABC为矩形,OA边在x轴上,OC边在y轴上.OB是矩形的对角线,点B的坐标是(8,4),点D在OA上,tan∠ABD=$\frac{3}{4}$.
如图,在平面直角坐标系中,点O是坐标原点,四边形OABC为矩形,OA边在x轴上,OC边在y轴上.OB是矩形的对角线,点B的坐标是(8,4),点D在OA上,tan∠ABD=$\frac{3}{4}$.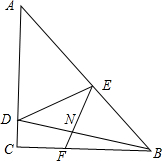 如图,在△ABC中,∠ACB=90°,AC=BC,在AC上取一点D,AB上取一点E,使∠BDC=∠EDA,过点E作EF⊥BD垂足为N,并与BC交于点F.若CF=4,AD=$\frac{11}{2}$,则CD=$\frac{3}{2}$.
如图,在△ABC中,∠ACB=90°,AC=BC,在AC上取一点D,AB上取一点E,使∠BDC=∠EDA,过点E作EF⊥BD垂足为N,并与BC交于点F.若CF=4,AD=$\frac{11}{2}$,则CD=$\frac{3}{2}$. 如图,△ABC内接于⊙O,已知AB=4cm,AC=3cm,BC边长的高AD长为2cm,则⊙O的半径为3cm.
如图,△ABC内接于⊙O,已知AB=4cm,AC=3cm,BC边长的高AD长为2cm,则⊙O的半径为3cm.