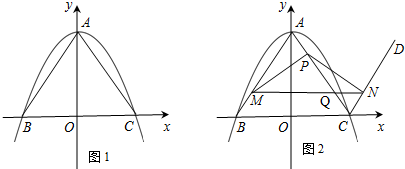��Ŀ����
4��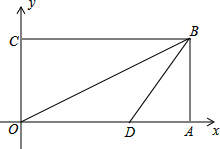 ��ͼ����ƽ��ֱ������ϵ�У���O������ԭ�㣬�ı���OABCΪ���Σ�OA����x���ϣ�OC����y���ϣ�OB�Ǿ��εĶԽ��ߣ���B�������ǣ�8��4������D��OA�ϣ�tan��ABD=$\frac{3}{4}$��
��ͼ����ƽ��ֱ������ϵ�У���O������ԭ�㣬�ı���OABCΪ���Σ�OA����x���ϣ�OC����y���ϣ�OB�Ǿ��εĶԽ��ߣ���B�������ǣ�8��4������D��OA�ϣ�tan��ABD=$\frac{3}{4}$����1�����D�����ꣻ
��2����P�ӵ�O������OA������ÿ��5����λ���ٶ������˶�������P��PQ��OB������Ϊ��Q������Q��QN��x�ύAB�ڵ�N����BD�ڵ�M����MN=y����y��t�ĺ�����ϵʽ����ֱ��д���Ա���t��ȡֵ��Χ��
��3���ڣ�2���������£���P���˶������У��Ƿ���ڵ�Q��ʹsin��AQD=$\frac{3}{5}$�������ڣ������Q�����ꣻ�������ڣ���˵�����ɣ�
���� ��1����B���������OA��AB�ij�����tan��ABD=$\frac{3}{4}$���AD�ij����Ӷ����OD�ij�������ȷ����D�����ꣻ
��2����AB��OA�ij������ù��ɶ������OB�ij������ݡ�POQ�ס�BOA���OQ=2$\sqrt{5}$t���Ӷ����BQ=4$\sqrt{5}$-2$\sqrt{5}$t��Ȼ�����ƽ���߷��߶γɱ��������������y=3-$\frac{3}{2}$t��0��t��2����
��3������������ֱ����Q�����꼴�ɣ�
���  �⣺��1����B��8��4����
�⣺��1����B��8��4����
��OA=8��AB=4��
��tan��ABD=$\frac{AD}{AB}$=$\frac{3}{4}$��
��AD=3��
��OD=OA-AD=8-3=5��
��D��5��0����
��2����ͼ1��ʾ��
��Rt��AOB��OA=8��AB=4��
���ݹ��ɶ����ã�OB=$\sqrt{O{A}^{2}+A{B}^{2}}$=4$\sqrt{5}$��
�ߡ�PQO=��BAO=90�㣬��POQ=��BOA��
���POQ�ס�BOA��
��$\frac{OQ}{OA}$=$\frac{OP}{OB}$����$\frac{OQ}{8}$=$\frac{5t}{4\sqrt{5}}$��
��OQ=2$\sqrt{5}$t��
��BQ=4$\sqrt{5}$-2$\sqrt{5}$t��
��QN��x�ᣬ
��$\frac{BN}{AB}$=$\frac{BQ}{OB}$=$\frac{MN}{AD}$=$\frac{4\sqrt{5}-2\sqrt{5}t}{4\sqrt{5}}$��
��$\frac{y}{3}$=1-$\frac{1}{2}$t��
��y=3-$\frac{3}{2}$t��0��t��2��
��3����ͼ2����t=1ʱ��P��D�غϣ�
��DQ��OB��BA��OA��
��A��B��Q��D�ĵ�����BDΪֱ����Բ�ϣ�
���AQD=��ABD��
��tan��AQD=tan��ABD=$\frac{AD}{AB}$=$\frac{3}{4}$��
��AD=3��AB=4��
��BD=5��
��OD=BD=5��
��Q��OB���е㣬
��Q��4��2����
��t=2ʱ��Q��B�غϣ���Q��8��4������Ȼtan��AQD=tan��ABD=$\frac{3}{4}$��
��0��t��2��
�൱Q��4��2��ʱ��sin��AQD=$\frac{3}{4}$��
���� ���⿼�����������ۺ��⣬�漰��֪ʶ�У�������Ǻ������壬������ͼ�����ʣ����ɶ�����ƽ���ߵ����ʣ����������ν�ϼ��������۵�˼�룬��������ʱע�⿼������Ҫȫ�棬�������ز�©��

| A�� | ��-3��2�� | B�� | ��3��2�� | C�� | ��-3��-2�� | D�� | ��3��-2�� |