题目内容
19．已知|2014-x|+$\sqrt{x-2015}$=x，求（x+2014）2．分析 利用负数没有平方根求出x的范围，将已知等式化简求出x的值，代入原式计算即可得到结果．
解答 解：∵x-2015≥0，即x≥2015，
∴2014-x＜0，
则|2014-x|+$\sqrt{x-2015}$=x-2014+$\sqrt{x-2015}$=x，即$\sqrt{x-2015}$=2014，
整理得：20142=x-2015，x=20142+2015，
则原式=（20142+2015+2014）2=20144+2×2014×4029+40292．
点评 此题考查了二次根式有意义的条件，做题时注意负数没有平方根．
练习册系列答案
相关题目
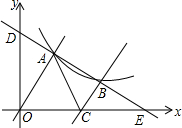已知直线y=-$\frac{2}{3}$x+6与双曲线y=$\frac{k}{x}$（x＞0）交于点A、B，把直线OA向右平移恰好经过点B，并与x轴交于点C，且OA：BC=2：1
如图所示，在等边三角形ABC中，AB=2，P是AB边上的任意一点（点P可以与点A重合，点不与点B重合），过点P作PE⊥BC，垂足为E，过点E作EF⊥AC，垂足为F，过点F作FQ⊥AB，垂足为Q，设BP=x，AQ=y．