题目内容
6. 图中△ABE和△ACD都是等边三角形.问AE与BD的大小关系是?如果要△ABE和△ACD全等,则还需要什么条件?
图中△ABE和△ACD都是等边三角形.问AE与BD的大小关系是?如果要△ABE和△ACD全等,则还需要什么条件?
分析 根据等边三角形性质推出AE=AB,AD=AC,∠EAB=∠DAC=60°,求出∠EAC=∠BAD,根据SAS证△AEC和△ABD全等即可;根据等边三角形的性质可以得到答案.
解答 解:EC=BD;
∵AE=AB,AC=AD,∠EAB=∠DAC=60°,
∴∠EAB+∠BAC=∠DAC+∠BAC,
即∠EAC=∠BAD,
在△AEC和△ABD中,
$\left\{\begin{array}{l}{AB=AE}\\{∠EAC=∠BAD}\\{AC=AD}\end{array}\right.$,
∴△ABD≌△AEC(SAS).
∴CE=BD,
∵△ABE和△ACD都是等边三角形
如果要△ABE和△ACD全等,只须AB=AC.
点评 此题考查了全等三角形的判定以及等边三角形的性质.此题难度适中,解题的关键是由题意证得∠EAC=∠BAD,注意数形结合思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.20150的值是( )
| A. | 2015 | B. | 0 | C. | 1 | D. | -1 |
15.下列各式计算正确的是( )
| A. | x6÷x2=x4 | B. | x2•x3=x6 | C. | (-x2)4=x6? | D. | x2+x3=x5 |
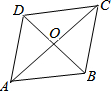 如图,?ABCD 的对角线AC,BD相交于点,且AC=4,BD=$2\sqrt{3}$,AB=$\sqrt{7}$.试证明四边形ABCD是菱形.
如图,?ABCD 的对角线AC,BD相交于点,且AC=4,BD=$2\sqrt{3}$,AB=$\sqrt{7}$.试证明四边形ABCD是菱形. 如图,菱形ABCD的边长为4,过点A,C作对角线AC的垂线,分别交CB和AD的延长线于点E,F,AE=3,则四边形AECF的周长为22.
如图,菱形ABCD的边长为4,过点A,C作对角线AC的垂线,分别交CB和AD的延长线于点E,F,AE=3,则四边形AECF的周长为22.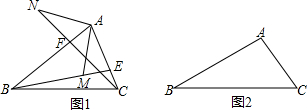

 如图,小雨把不等式3x+1>2(x-1)的解集表示在数轴上,则阴影部分盖住的数字是-3.
如图,小雨把不等式3x+1>2(x-1)的解集表示在数轴上,则阴影部分盖住的数字是-3.