题目内容
1. 如图,CD=AB,AE=CF,DE=BF,求证:AB∥CD.
如图,CD=AB,AE=CF,DE=BF,求证:AB∥CD.
分析 首先利用SSS证得△ADE≌△CBF,得出∠AED=∠BFC,而CE=AF,进一步证得△ABF≌△DCE,则∠BAF=∠DCE,然后根据平行线的判定即可得到结论.
解答 证明:∵在△ADE和△CBF中,
$\left\{\begin{array}{l}{CD=AB}\\{AE=CF}\\{DE=BF}\end{array}\right.$,
∴△ADE≌△CBF,
∴∠AED=∠BFC,
∴∠DEC=∠AFB,
∵AE=CF,
∴AF=CE,
在△ABF和△DCE中,
$\left\{\begin{array}{l}{DE=BF}\\{∠DEC=∠AFB}\\{CE=AF}\end{array}\right.$
∴△DCE≌△ABF,
∴∠DCE=∠BAF,
∴AB∥CD.
点评 本题考查了全等三角形的判定与性质:有两边和它们的夹角对应相等的两个三角形全等;全等三角形的对应角相等.也考查了平行线的判定.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
6.已知双曲线y=$\frac{k-1}{x}$过点A(1,1),那么过点A的直线y=kx+b经过( )
| A. | 一、二、三象限 | B. | 一、二、四象限 | C. | 一、三、四象限 | D. | 二、三、四象限 |

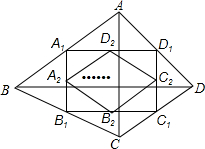 如图,四边形ABCD中,AC=a,BD=b,且AC⊥BD,顺次连接四边形ABCD各边中点,得到四边形A1B1C1D1,再顺次连接四边形A1B1C1D1各边中点,得到四边形A2B2C2D2,…,如此进行下去,得到四边形AnBnCnDn.下列结论正确的有( )
如图,四边形ABCD中,AC=a,BD=b,且AC⊥BD,顺次连接四边形ABCD各边中点,得到四边形A1B1C1D1,再顺次连接四边形A1B1C1D1各边中点,得到四边形A2B2C2D2,…,如此进行下去,得到四边形AnBnCnDn.下列结论正确的有( )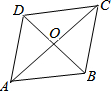 如图,?ABCD 的对角线AC,BD相交于点,且AC=4,BD=$2\sqrt{3}$,AB=$\sqrt{7}$.试证明四边形ABCD是菱形.
如图,?ABCD 的对角线AC,BD相交于点,且AC=4,BD=$2\sqrt{3}$,AB=$\sqrt{7}$.试证明四边形ABCD是菱形. 如图,已知四边形ABCD中,AC=BD,E、F、G、H分别是AB、BC、CD、DA边上的中点.
如图,已知四边形ABCD中,AC=BD,E、F、G、H分别是AB、BC、CD、DA边上的中点.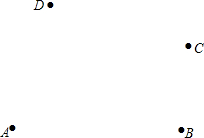 如图,平面上有A、B、C、D四点
如图,平面上有A、B、C、D四点