题目内容
13.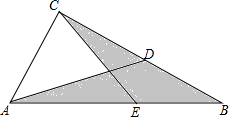 在△ABC中,AE=2EB,D为BC的中点,△ACD的面积为$\frac{1}{4}$,△BCE的面积为$\frac{1}{6}$,求阴影部分的面积.
在△ABC中,AE=2EB,D为BC的中点,△ACD的面积为$\frac{1}{4}$,△BCE的面积为$\frac{1}{6}$,求阴影部分的面积.
分析 设AD,CE相交于F,连接BF,由D为BC的中点,于是得到S△CDF=S△BDF=S1,由于AE=2EB,求得S△AEF=2S△BEF,然后根据已知条件得方程组,即可得到结果.
解答  解:如图:设AD,CE相交于F,连接BF,
解:如图:设AD,CE相交于F,连接BF,
∵D为BC的中点,
∴S△CDF=S△BDF=S1,
∵AE=2EB,
∴S△AEF=2S△BEF,
设S△BEF=S2,则S△AEF=2S2,
由题意得$\left\{\begin{array}{l}{2{S}_{1}{+S}_{2}=\frac{1}{6}}\\{{S}_{1}+3{S}_{2}=\frac{1}{4}}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{{S}_{1}=\frac{1}{15}}\\{{S}_{2}=\frac{1}{20}}\end{array}\right.$,
∴S阴影=2S1+3S2=$\frac{3}{10}$.
点评 本题考查了三角形的面积的求法,熟练掌握等高三角形的面积的比等于底的比是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
3.某商场一天中售出李宁运动鞋11双,其中各种尺码的鞋的销售量如下表所示,
那么这11双鞋的尺码组成的一组数据中,众数与中位数分别为( )
| 鞋的尺码(单位:cm) | 23.5 | 24 | 24.5 | 25 | 26 |
| 销售量(单位:双) | 1 | 2 | 2 | 5 | 1 |
| A. | 25,24.5 | B. | 24.5,25 | C. | 26,25 | D. | 25,25 |
19.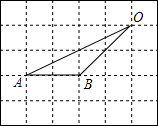 如图,在网格中,小正方形的边长均为1,点A、B、O都在格点上,则∠AOB的正弦值是( )
如图,在网格中,小正方形的边长均为1,点A、B、O都在格点上,则∠AOB的正弦值是( )
 如图,在网格中,小正方形的边长均为1,点A、B、O都在格点上,则∠AOB的正弦值是( )
如图,在网格中,小正方形的边长均为1,点A、B、O都在格点上,则∠AOB的正弦值是( )| A. | $\frac{10\sqrt{10}}{3}$ | B. | $\frac{\sqrt{10}}{10}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
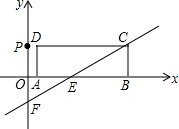 已知长方形ABCD的边长AB=9,AD=3,现将此长方形置于平面直角坐标系中,使AB在x轴的正半轴上,经过点C的直线y=$\frac{1}{2}$x-2与x轴交于点E,与y轴交于点F.
已知长方形ABCD的边长AB=9,AD=3,现将此长方形置于平面直角坐标系中,使AB在x轴的正半轴上,经过点C的直线y=$\frac{1}{2}$x-2与x轴交于点E,与y轴交于点F.