题目内容
4.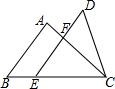 如图,已知△ABC和△DEC的面积相等,点E在BC边上,DE∥AB交AC于点F,AB=12,EF=9,则DF的长是7.
如图,已知△ABC和△DEC的面积相等,点E在BC边上,DE∥AB交AC于点F,AB=12,EF=9,则DF的长是7.
分析 方法1,根据题意,易得△CDF与四边形AFEB的面积相等,再根据相似三角形的相似比求得它们的面积关系比,从而求DF的长.
方法2,利用相似三角形的性质和三角形的面积相等即可得出结论.
解答 解:方法1,∵△ABC与△DEC的面积相等,
∴△CDF与四边形AFEB的面积相等,
∵AB∥DE,
∴△CEF∽△CBA,
∵EF=9,AB=12,
∴EF:AB=9:12=3:4,
∴△CEF和△CBA的面积比=9:16,
设△CEF的面积为9k,则四边形AFEB的面积=7k,
∵△CDF与四边形AFEB的面积相等,
∴S△CDF=7k,
∵△CDF与△CEF是同高不同底的三角形,
∴面积比等于底之比,
∴DF:EF=7k:9k,
∴DF=7.
故答案为:7.
方法2,如图,
过点A作AM⊥BC,过点D作DN⊥BC,
∵DE∥AB,
∴△ABC∽△FEC,
∴$\frac{BC}{EC}=\frac{AB}{EF}$=$\frac{4}{3}$,
∵S△ABC=S△DEC,
∴$\frac{1}{2}$BC×AM=$\frac{1}{2}$EC×DN,
∴$\frac{AM}{DN}=\frac{3}{4}$,
∵AB∥DE,
∴△ABM∽DEN,
∴$\frac{AB}{DE}=\frac{AM}{DN}$,
∴$\frac{12}{DE}=\frac{3}{4}$,
∴DE=16,
∴DF=DE-EF=7,
故答案为:7.
点评 此题考查了相似三角形的判定与性质,解题的关键是会用割补法计算面积.

练习册系列答案
相关题目
14.某组数据-5,3,-8,9,0,3的极差和众数分别是( )
| A. | -8,9 | B. | 17,9 | C. | 17,3 | D. | 0,3 |
15.李华根据演讲比赛中九位评委所给的分数制作了表格:
对9个评委所给的分数,去掉一个最高分和一个最低分后,表中数据一定不发生变化的是( )
| 平均数 | 中位数 | 众数 | 方差 |
| 8.5分 | 8.3分 | 8.1分 | 0.15 |
| A. | 平均数 | B. | 中位数 | C. | 方差 | D. | 众敎 |
12.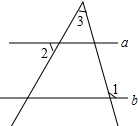 如图,直线a∥b,∠1=110°,∠2=50°,则∠3的度数为( )
如图,直线a∥b,∠1=110°,∠2=50°,则∠3的度数为( )
 如图,直线a∥b,∠1=110°,∠2=50°,则∠3的度数为( )
如图,直线a∥b,∠1=110°,∠2=50°,则∠3的度数为( )| A. | 50° | B. | 60° | C. | 70° | D. | 110° |
19.下列运算正确的是( )
| A. | $\sqrt{25}=±5$ | B. | $\root{3}{-8}=-2$ | C. | $\sqrt{12}=3\sqrt{2}$ | D. | $3\sqrt{2}-2\sqrt{2}=1$ |
9.若正比例函数y=kx的图象经过点(2,-6),则k的值为( )
| A. | -3 | B. | -$\frac{1}{3}$ | C. | 3 | D. | $\frac{1}{3}$ |
16.甲、乙、丙、丁四位同学参加了10次数学测验,他们测验的平均成绩($\overline{x}$)与方差(S2)如下表所示,那么这四位同学中,成绩较好,且较稳定的是( )
| 甲 | 乙 | 丙 | 丁 | |
| $\overline{x}$ | 85 | 90 | 90 | 85 |
| S2 | 1.0 | 1.0 | 1.2 | 1.8 |
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
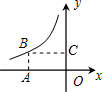 如图,矩形OABC上,点A、C分别在x、y轴上,点B在反比例y=$\frac{k}{x}$位于第二象限的图象上,矩形面积为6,则k的值是( )
如图,矩形OABC上,点A、C分别在x、y轴上,点B在反比例y=$\frac{k}{x}$位于第二象限的图象上,矩形面积为6,则k的值是( )