题目内容
8.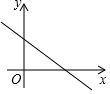 如图是一次函数y=ax+b(a≠0)的大致图象,则下列结论正确的是( )
如图是一次函数y=ax+b(a≠0)的大致图象,则下列结论正确的是( )| A. | a>0,b>0 | B. | a>0,b<0 | C. | a<0,b>0 | D. | a<0,b<0 |
分析 根据一次函数图象与系数的关系进行判断.
解答  解:该函数图象经过第一、三象限,则a<0,
解:该函数图象经过第一、三象限,则a<0,
该直线与y轴交于正半轴,则b>0,
综上所述,a<0,b>0.
故选:C.
点评 考查了次函数的图象与系数的关系:由于y=kx+b与y轴交于(0,b),当b>0时,(0,b)在y轴的正半轴上,直线与y轴交于正半轴;当b<0时,(0,b)在y轴的负半轴,直线与y轴交于负半轴.
①k>0,b>0?y=kx+b的图象在一、二、三象限;
②k>0,b<0?y=kx+b的图象在一、三、四象限;
③k<0,b>0?y=kx+b的图象在一、二、四象限;
④k<0,b<0?y=kx+b的图象在二、三、四象限.

练习册系列答案
相关题目
18.在数学竞赛的选拔活动中,对甲、乙两名同学的成绩经过统计分析可得:$\overline{{x}_{甲}}$=94(分),$\overline{{x}_{乙}}$=94(分);S${\;}_{甲}^{2}$=1.02,S${\;}_{乙}^{2}$=0.85,下列结论正确的是( )
| A. | 甲的成绩比乙的成绩好 | B. | 甲的成绩比乙的成绩稳定 | ||
| C. | 应该选择乙同学参加竞赛 | D. | 不能衡量两名同学的成绩优劣 |
19.下列根式中,最简二次根式是( )
| A. | $\sqrt{18}$ | B. | $\sqrt{24}$ | C. | $\sqrt{30}$ | D. | $\sqrt{36}$ |
16.下列命题中,原命题是假命题,而逆命题是真命题的是( )
| A. | 两个全等三角形的面积相等 | |
| B. | 两条高线相等的三角形是等腰三角形 | |
| C. | 相等的角是对顶角 | |
| D. | 线段的垂直平分线上的点到线段两端点距离相等 |
13. 如图,直线a∥b,直角三角板的直角顶点在直线b上,一条直角边与直线a所形成的∠1=55°,则另外一条直角边与直线b所形成的∠2的度数为( )
如图,直线a∥b,直角三角板的直角顶点在直线b上,一条直角边与直线a所形成的∠1=55°,则另外一条直角边与直线b所形成的∠2的度数为( )
 如图,直线a∥b,直角三角板的直角顶点在直线b上,一条直角边与直线a所形成的∠1=55°,则另外一条直角边与直线b所形成的∠2的度数为( )
如图,直线a∥b,直角三角板的直角顶点在直线b上,一条直角边与直线a所形成的∠1=55°,则另外一条直角边与直线b所形成的∠2的度数为( )| A. | 25° | B. | 30° | C. | 35° | D. | 40° |
20.下列计算中错误的有( )
①4a3b÷2a2=2a,②-12x4y3÷2x2y=6x2y2,③-16a2bc÷$\frac{1}{4}$a2b=-4c,④(-$\frac{1}{2}$ab2)3÷(-$\frac{1}{2}$ab2)=$\frac{1}{4}$a2b4.
①4a3b÷2a2=2a,②-12x4y3÷2x2y=6x2y2,③-16a2bc÷$\frac{1}{4}$a2b=-4c,④(-$\frac{1}{2}$ab2)3÷(-$\frac{1}{2}$ab2)=$\frac{1}{4}$a2b4.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
17. 如图,点D,E,F分别是AB,BC,CA上的点,且AE,BF,CD交于点O,它们将△ABC分成6个面积相等的三角形,则AE,BF,CD一定是△ABC的( )
如图,点D,E,F分别是AB,BC,CA上的点,且AE,BF,CD交于点O,它们将△ABC分成6个面积相等的三角形,则AE,BF,CD一定是△ABC的( )
 如图,点D,E,F分别是AB,BC,CA上的点,且AE,BF,CD交于点O,它们将△ABC分成6个面积相等的三角形,则AE,BF,CD一定是△ABC的( )
如图,点D,E,F分别是AB,BC,CA上的点,且AE,BF,CD交于点O,它们将△ABC分成6个面积相等的三角形,则AE,BF,CD一定是△ABC的( )| A. | 高 | B. | 中线 | ||
| C. | 角平分线 | D. | 三边的垂直平分线 |
18.若函数y=kx的图象经过点(-1,2),则k的值是( )
| A. | -2 | B. | 2 | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |