题目内容
13．
如图，直线a∥b，直角三角板的直角顶点在直线b上，一条直角边与直线a所形成的∠1=55°，则另外一条直角边与直线b所形成的∠2的度数为（ ）| A． | 25° | B． | 30° | C． | 35° | D． | 40° |
分析 先由直线a∥b，根据平行线的性质，得出∠3=∠1=55°，再由已知直角三角板得∠4=90°，然后由∠2+∠3+∠4=180°，求出∠2．
解答 
解：∵直线a∥b，
∴∠3=∠1=55°，
∵∠4=90°，∠2+∠3+∠4=180°，
∴∠2=180°-55°-90°=35°．
故选：C．
点评 此题考查了学生对平行线性质的应用，解决问题的关键是由平行线性质得出同位角相等．
练习册系列答案
教材全解字词句篇系列答案
相关题目
3．在一个不透明的盒子里装有4个分别写有数字-3、-2、-1、0的小球，它们除数字不同外其余全部相同，现从盒子里随机取出一个小球，记下数字a后放回，再取出一个记下数字b，那么点（a，b）在抛物线y=-x2+1上的概率是（ ）
| A． | $\frac{1}{8}$ | B． | $\frac{1}{6}$ | C． | $\frac{3}{16}$ | D． | $\frac{1}{4}$ |
4．
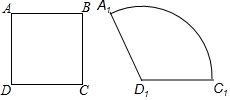如图，用两根等长的金属丝，各自首尾相接，分别围成正方形ABCD和扇形A1D1C1，使A1D1=AD，正方形面积为P，扇形面积为Q，那么P和Q的关系是（ ）
如图，用两根等长的金属丝，各自首尾相接，分别围成正方形ABCD和扇形A1D1C1，使A1D1=AD，正方形面积为P，扇形面积为Q，那么P和Q的关系是（ ）| A． | P＜Q | B． | P=Q | C． | P＞Q | D． | 无法确定 |
1．李克强总理在2017年政府工作报告中指出，扎实推进新型城镇化，深化户籍制度改革，今年实现进城落户1300万人以上，其中1300万用科学记数法表示为（ ）
| A． | 1.3×107 | B． | 1.3×106 | C． | 0.13×108 | D． | 1.3×108 |
8．
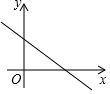如图是一次函数y=ax+b（a≠0）的大致图象，则下列结论正确的是（ ）
如图是一次函数y=ax+b（a≠0）的大致图象，则下列结论正确的是（ ）| A． | a＞0，b＞0 | B． | a＞0，b＜0 | C． | a＜0，b＞0 | D． | a＜0，b＜0 |
18．一次函数y=（m-1）x+2的图象过点（-2，2），m的值是（ ）
| A． | -1 | B． | 1 | C． | 2 | D． | 3 |
5．
如图，AB∥CD，点E，F分别在BD，CD上，EF⊥BD，∠1=48°，则∠2的度数为（ ）
如图，AB∥CD，点E，F分别在BD，CD上，EF⊥BD，∠1=48°，则∠2的度数为（ ）| A． | 96° | B． | 48° | C． | 42° | D． | 24° |
2．下面的图形中，既是轴对称图形又是中心对称图形的是（ ）
| A． |  | B． |  | C． |  | D． |  |
3．下列各式化简结果为有理数的是（ ）
| A． | $\sqrt{2}$ | B． | （$\sqrt{3}$-1）2 | C． | $\frac{π}{3}$ | D． | $\root{3}{-8}$ |