题目内容
15.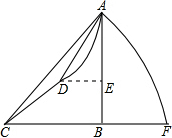 小明在山脚C处测得山顶A的仰角为45°,他沿坡角为37°的斜坡前进200米到达D处,测得山顶A的仰角为53°,求山高AB(A、B、C、D、E、F在一个平面内)参考数据:sin37°=cos53°≈$\frac{3}{5}$,cos37°=sin53°≈$\frac{4}{5}$,tan53°≈$\frac{4}{3}$.
小明在山脚C处测得山顶A的仰角为45°,他沿坡角为37°的斜坡前进200米到达D处,测得山顶A的仰角为53°,求山高AB(A、B、C、D、E、F在一个平面内)参考数据:sin37°=cos53°≈$\frac{3}{5}$,cos37°=sin53°≈$\frac{4}{5}$,tan53°≈$\frac{4}{3}$.
分析 作DF⊥CF,垂足为F,作DE⊥AB于点E,先判断出△ACD的形状,再由锐角三角函数的定义即可得出结论.
解答  解:作DF⊥CF,垂足为F,作DE⊥AB于点E.
解:作DF⊥CF,垂足为F,作DE⊥AB于点E.
∵∠ACB=45°,∠DCB=37°,
∴∠ACD=45°-37°=8°,∠CAB=45°,AB=BC..
∵∠ADE=53°,
∴∠DAE=90°-53°=37°,
∴∠CAD=45°-37°=8°,
∴AD=CD=200米.
在Rt△CDF中,CF=CD•cos37°=200×$\frac{4}{5}$=160(米).
在Rt△ADE中,DE=AD•cos53°=200×$\frac{3}{5}$=120(米).
∵DF⊥CF,EB⊥CF,DE⊥AB,
∴四边形DEBF是矩形,
∴DE=BF,
∴AB=BC=160+120=280(米).
答:山高AB是280米.
点评 本题考查的是解直角三角形的应用-仰角俯角问题,熟记锐角三角函数的定义是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 在全民健身环城越野赛中,甲乙两选手的行程y(千米)随时间x(时)变化的图象(全程)如图所示,有下列说法:①起跑后1小时内,甲在乙的前面;②第1小时两人都跑了10千米;③甲比乙先到达终点;④两人都跑了20千米.其中正确的说法是( )
在全民健身环城越野赛中,甲乙两选手的行程y(千米)随时间x(时)变化的图象(全程)如图所示,有下列说法:①起跑后1小时内,甲在乙的前面;②第1小时两人都跑了10千米;③甲比乙先到达终点;④两人都跑了20千米.其中正确的说法是( )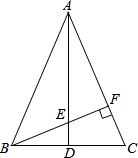 如图,△ABC中,AD⊥BC,BE的延长线交AC于点F,且BF⊥AC于F,∠BAC=45°,试证明:△AEF≌△BCF.
如图,△ABC中,AD⊥BC,BE的延长线交AC于点F,且BF⊥AC于F,∠BAC=45°,试证明:△AEF≌△BCF.