题目内容
12. 如图,矩形ABCD的长和宽分别为6和4,E、F、G、H依次是矩形ABCD各边的中点,则四边形EFGH的周长等于4$\sqrt{13}$.
如图,矩形ABCD的长和宽分别为6和4,E、F、G、H依次是矩形ABCD各边的中点,则四边形EFGH的周长等于4$\sqrt{13}$.
分析 直接利用矩形的性质结合勾股定理得出EF,FG,EH,HG的长即可得出答案.
解答 解:∵矩形ABCD的长和宽分别为6和4,E、F、G、H依次是矩形ABCD各边的中点,
∴AE=BE=CG=DG=2,AH=DH=BF=FC=3,
∴EH=EF=HG=GF=$\sqrt{{2}^{2}+{3}^{2}}$=$\sqrt{13}$,
∴四边形EFGH的周长等于4$\sqrt{13}$.
故答案为:4$\sqrt{13}$.
点评 此题主要考查了中点四边形以及勾股定理,正确应用勾股定理是解题关键.

练习册系列答案
相关题目
20.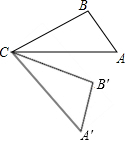 如图,将△ABC绕着点C顺时针旋转50°后得到△A′B′C′,若∠A=40°,∠B′=110°,则∠A′CB的度数是( )
如图,将△ABC绕着点C顺时针旋转50°后得到△A′B′C′,若∠A=40°,∠B′=110°,则∠A′CB的度数是( )
 如图,将△ABC绕着点C顺时针旋转50°后得到△A′B′C′,若∠A=40°,∠B′=110°,则∠A′CB的度数是( )
如图,将△ABC绕着点C顺时针旋转50°后得到△A′B′C′,若∠A=40°,∠B′=110°,则∠A′CB的度数是( )| A. | 110° | B. | 80° | C. | 40° | D. | 30° |
2.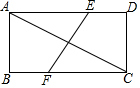 如图,矩形ABCD中,AB=3,BC=4,若将矩形折叠,使C点与A点重合,则EF( )
如图,矩形ABCD中,AB=3,BC=4,若将矩形折叠,使C点与A点重合,则EF( )
 如图,矩形ABCD中,AB=3,BC=4,若将矩形折叠,使C点与A点重合,则EF( )
如图,矩形ABCD中,AB=3,BC=4,若将矩形折叠,使C点与A点重合,则EF( )| A. | $\frac{7}{4}$ | B. | $\frac{15}{4}$ | C. | $\frac{15}{2}$ | D. | $\frac{7}{2}$ |
 如图,菱形ABCD的对角线相交于O,若AB=5,OA=4,则BD=6.
如图,菱形ABCD的对角线相交于O,若AB=5,OA=4,则BD=6. 如图,在所给网格图( 每小格均为边长是1的正方形)中完成下列各题:
如图,在所给网格图( 每小格均为边长是1的正方形)中完成下列各题: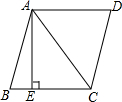 如图,在菱形ABCD中,AB=10,对角线AC=12,过点A作AE⊥BC,垂足为E,则AE的长为$\frac{48}{5}$.
如图,在菱形ABCD中,AB=10,对角线AC=12,过点A作AE⊥BC,垂足为E,则AE的长为$\frac{48}{5}$.