��Ŀ����
11��ij�н���������ʵ��������ԣ�����ѧ����ǩ�ķ�ʽ�����Լ��Ŀ������ݣ��涨��ÿ����������������ʵ�飨��ǩ�ֱ��ô���W1��W2��W3��ʾ����������ѧʵ���⣨��ǩ�ֱ��ô���H1��H2��ʾ������������ʵ�飨��ǩ�ֱ��ô���S1��S2��ʾ���зֱ��ȡһ�����п��ԣ�С���ڿ�������ǩ������£�������������ĸ���ȡһ����ǩ����1��ֱ��д����ǡ�ó鵽H2�������
��2����С���鵽����ǩ�Ĵ�����±꣨���硰W2�����±��ǡ�2����֮��Ϊ5�ĸ��ʣ�
���� ��1��ֱ�Ӹ��ݸ��ʹ�ʽ��⣻
��2���Ȼ�����״ͼչʾ����12�ֵȿ��ܵĽ���������ҳ���ǩ�Ĵ�����±꣨���硰W2�����±��ǡ�2����֮��Ϊ5�Ľ������Ȼ����ݸ��ʹ�ʽ���㣮
��� �⣺��1����ǡ�ó鵽H2�ĸ���=$\frac{1}{2}$��
��2������״ͼΪ��
����12�ֵȿ��ܵĽ������������ǩ�Ĵ�����±꣨���硰W2�����±��ǡ�2����֮��Ϊ5�Ľ����Ϊ4��
����С���鵽����ǩ�Ĵ�����±꣨���硰W2�����±��ǡ�2����֮��Ϊ5�ĸ���=$\frac{4}{12}$=$\frac{1}{3}$��
���� ���⿼�����б�������״ͼ����ͨ���б�������״ͼ��չʾ���еȿ��ܵĽ�����n���ٴ���ѡ�������¼�A��B�Ľ����Ŀm��Ȼ����ݸ��ʹ�ʽ����¼�A��B�ĸ��ʣ�

��ϰ��ϵ�д�
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
�����Ŀ
1�����м�����ȷ���ǣ�������
| A�� | -$\sqrt{��-1��^{2}}$=1 | B�� | -2+1=1 | C�� | 2����-1��0=-2 | D�� | 9-1��9=1 |
19�����м�����ȷ���ǣ�������
| A�� | m3-m2=m | B�� | m3-m2=m5 | C�� | ��m+n��2=m2+n2 | D�� | ��m3��2=m6 |
20�������������ʵ��a��b���������㡰������ʹ����ʽ�ӳ�����1��2=-$\frac{3}{2}$��2��1=$\frac{3}{2}$����-2����5=$\frac{21}{10}$��5����-2��=-$\frac{21}{10}$��������-3������-4��=��������
| A�� | -$\frac{7}{12}$ | B�� | $\frac{7}{12}$ | C�� | -$\frac{25}{12}$ | D�� | $\frac{25}{12}$ |
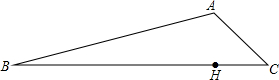 2015��4��25�գ��Ჴ������8.1��������֪A������ε������������أ����мס�������С�ֶӷֱ�ͬʱ��B��C���س���ǰ��A�ؾ�Ԯ��������·BA�н���������·CA�н�����֪C��A����ƫ��55�㷽��AB���¶�Ϊ1��5��ͬʱ���ڵ���ԭ�����BC·����ʯ��������BC·����λ��A�����Ϸ�������һ���ϴ�H���������BC·�ϣ���֪BHΪ12000m��
2015��4��25�գ��Ჴ������8.1��������֪A������ε������������أ����мס�������С�ֶӷֱ�ͬʱ��B��C���س���ǰ��A�ؾ�Ԯ��������·BA�н���������·CA�н�����֪C��A����ƫ��55�㷽��AB���¶�Ϊ1��5��ͬʱ���ڵ���ԭ�����BC·����ʯ��������BC·����λ��A�����Ϸ�������һ���ϴ�H���������BC·�ϣ���֪BHΪ12000m��