题目内容
15.分解因式:y3-4y2+4y=( )| A. | y(y2-4y+4) | B. | y(y-2)2 | C. | y(y+2)2 | D. | y(y+2)(y-2) |
分析 原式提取y,再利用完全平方公式分解即可.
解答 解:原式=y(y2-4y+4)=y(y-2)2,
故选B
点评 此题考查了提公式法与公式法的综合运用,要注意有没有分解到不能分解.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
20.对于任意非零实数a、b,定义运算“⊕”,使下列式子成立:1⊕2=-$\frac{3}{2}$,2⊕1=$\frac{3}{2}$,(-2)⊕5=$\frac{21}{10}$,5⊕(-2)=-$\frac{21}{10}$,…,则(-3)⊕(-4)=( )
| A. | -$\frac{7}{12}$ | B. | $\frac{7}{12}$ | C. | -$\frac{25}{12}$ | D. | $\frac{25}{12}$ |
5. 如图,四个小正方形拼成的大正方形,A、B、O是小正方形的顶点,P是以OA为半径的⊙O上的点,且位于右上方的小正方形内,则∠APB等于( )
如图,四个小正方形拼成的大正方形,A、B、O是小正方形的顶点,P是以OA为半径的⊙O上的点,且位于右上方的小正方形内,则∠APB等于( )
 如图,四个小正方形拼成的大正方形,A、B、O是小正方形的顶点,P是以OA为半径的⊙O上的点,且位于右上方的小正方形内,则∠APB等于( )
如图,四个小正方形拼成的大正方形,A、B、O是小正方形的顶点,P是以OA为半径的⊙O上的点,且位于右上方的小正方形内,则∠APB等于( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
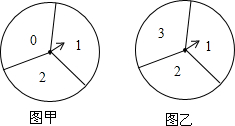 在如图的甲、乙两个转盘中,指针指向每一个数字的机会是均等的,转动甲转盘,转盘停止转动后,指针所指的数字记为x,转动乙转盘,转盘停止转动后,指针所指的数字记为y,同时转动两个转盘,当转盘停止转动后,指针所指的两个数字用来表示一个点的坐标,记为(x,y),那么该点在坐标轴上的概率是$\frac{1}{3}$.
在如图的甲、乙两个转盘中,指针指向每一个数字的机会是均等的,转动甲转盘,转盘停止转动后,指针所指的数字记为x,转动乙转盘,转盘停止转动后,指针所指的数字记为y,同时转动两个转盘,当转盘停止转动后,指针所指的两个数字用来表示一个点的坐标,记为(x,y),那么该点在坐标轴上的概率是$\frac{1}{3}$. 如图所示,在平行四边形ABCD中,分别以AB、AD为边作等边△ABE和等边△ADF,分别连接CE、CF和EF,则下列结论中一定成立的是①②③(把所有正确结论的序号都填在横线上).
如图所示,在平行四边形ABCD中,分别以AB、AD为边作等边△ABE和等边△ADF,分别连接CE、CF和EF,则下列结论中一定成立的是①②③(把所有正确结论的序号都填在横线上).