题目内容
1.若实数x、y满足x2=$\sqrt{\frac{1}{2}y-\frac{1}{2}}$+$\sqrt{3-3y}$+4,则x+y的值是( )| A. | 3或-3 | B. | 3或-1 | C. | -3或-1 | D. | 3或1 |
分析 根据被开方数大于等于0列式求出y,再求出x,然后相加计算即可得解.
解答 解:由题意得,$\frac{1}{2}$y-$\frac{1}{2}$≥0且3-3y≥0,
解得y≥1且y≤1,
所以,y=1,
x2=4,
所以,x=±2,
x+y=2+1=3,
或x+y=-2+1=-1,
综上所述,x+y的值是3或-1.
故选B.
点评 本题考查了二次根式有意义的条件,二次根式中的被开方数必须是非负数,否则二次根式无意义.

练习册系列答案
相关题目
11. 如图.已知直线a,b被直线c所截,且a∥b,∠1=42°,那么∠2的度数为( )
如图.已知直线a,b被直线c所截,且a∥b,∠1=42°,那么∠2的度数为( )
 如图.已知直线a,b被直线c所截,且a∥b,∠1=42°,那么∠2的度数为( )
如图.已知直线a,b被直线c所截,且a∥b,∠1=42°,那么∠2的度数为( )| A. | 42° | B. | 48° | C. | 52° | D. | 132° |
9.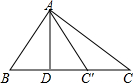 如图,△ABC中,已知BC=16,高AD=10,动点C′由点C沿CB向点B移动(不与点B重合).设CC′的长为x,△ABC′的面积为S,则S与x之间的函数关系式为( )
如图,△ABC中,已知BC=16,高AD=10,动点C′由点C沿CB向点B移动(不与点B重合).设CC′的长为x,△ABC′的面积为S,则S与x之间的函数关系式为( )
 如图,△ABC中,已知BC=16,高AD=10,动点C′由点C沿CB向点B移动(不与点B重合).设CC′的长为x,△ABC′的面积为S,则S与x之间的函数关系式为( )
如图,△ABC中,已知BC=16,高AD=10,动点C′由点C沿CB向点B移动(不与点B重合).设CC′的长为x,△ABC′的面积为S,则S与x之间的函数关系式为( )| A. | S=80-5x | B. | S=5x | C. | S=10x | D. | S=5x+80 |
16.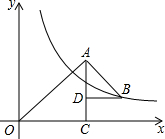 如图,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数y=$\frac{k}{x}$在第一象限的图象经过点B,若OA2-AB2=12,则k的值为( )
如图,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数y=$\frac{k}{x}$在第一象限的图象经过点B,若OA2-AB2=12,则k的值为( )
 如图,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数y=$\frac{k}{x}$在第一象限的图象经过点B,若OA2-AB2=12,则k的值为( )
如图,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数y=$\frac{k}{x}$在第一象限的图象经过点B,若OA2-AB2=12,则k的值为( )| A. | 4 | B. | 6 | C. | 8 | D. | 12 |
13.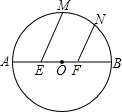 如图,半圆O的直径为AB,E,F为AB的三等分点.EM∥FN交半圆于M,N,且∠NFB=60°,EM+FN=$\sqrt{33}$,则它的半径是( )
如图,半圆O的直径为AB,E,F为AB的三等分点.EM∥FN交半圆于M,N,且∠NFB=60°,EM+FN=$\sqrt{33}$,则它的半径是( )
 如图,半圆O的直径为AB,E,F为AB的三等分点.EM∥FN交半圆于M,N,且∠NFB=60°,EM+FN=$\sqrt{33}$,则它的半径是( )
如图,半圆O的直径为AB,E,F为AB的三等分点.EM∥FN交半圆于M,N,且∠NFB=60°,EM+FN=$\sqrt{33}$,则它的半径是( )| A. | 2$\sqrt{2}$ | B. | 3$\sqrt{2}$ | C. | 4 | D. | 3 |
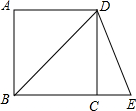 如图,正方形ABCD中,AB=3,延长BC至E,使BE=BD,则△BDE的面积为$\frac{9}{2}\sqrt{2}$.
如图,正方形ABCD中,AB=3,延长BC至E,使BE=BD,则△BDE的面积为$\frac{9}{2}\sqrt{2}$.