题目内容
6.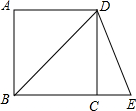 如图,正方形ABCD中,AB=3,延长BC至E,使BE=BD,则△BDE的面积为$\frac{9}{2}\sqrt{2}$.
如图,正方形ABCD中,AB=3,延长BC至E,使BE=BD,则△BDE的面积为$\frac{9}{2}\sqrt{2}$.
分析 根据正方形的性质得出BD=$3\sqrt{2}$,进而根据BE=BD得出CE=$3\sqrt{2}-3$,得出△DCE的面积,再计算出△BCD的面积,两面积相加即可.
解答 解:∵四边形ABCD是正方形,AB=3,
∴BD=BE=$3\sqrt{2}$,
∴CE=BE-BC=$3\sqrt{2}-3$,
∴△DCE的面积=$\frac{1}{2}×(3\sqrt{2}-3)×3=\frac{9}{2}\sqrt{2}-\frac{9}{2}$,
∵△BCD的面积=$\frac{1}{2}×3×3=\frac{9}{2}$,
∴△BDE的面积=△DCE的面积+△BCD的面积
=$\frac{9}{2}\sqrt{2}-\frac{9}{2}+\frac{9}{2}=\frac{9}{2}\sqrt{2}$,
故答案为:$\frac{9}{2}\sqrt{2}$.
点评 本题考查了正方形的性质,三角形面积的计算,熟记各性质并准确识图是解题的关键.

练习册系列答案
相关题目
1.若实数x、y满足x2=$\sqrt{\frac{1}{2}y-\frac{1}{2}}$+$\sqrt{3-3y}$+4,则x+y的值是( )
| A. | 3或-3 | B. | 3或-1 | C. | -3或-1 | D. | 3或1 |
 将一个直角三角板和一把直尺如图放置,如果∠α=44°,则∠β的度数是46°.
将一个直角三角板和一把直尺如图放置,如果∠α=44°,则∠β的度数是46°.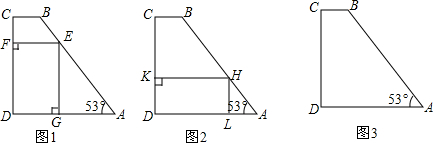
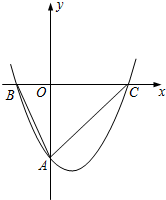 如图,已知抛物线y=ax2+bx+c经过点A(0,-4),点B(-2,0),点C(4,0).
如图,已知抛物线y=ax2+bx+c经过点A(0,-4),点B(-2,0),点C(4,0). 已知:如图,矩形ABCD的对角线AB、BD相交于点O,DE∥CA,AE∥BD.求证:四边形AODE是菱形.
已知:如图,矩形ABCD的对角线AB、BD相交于点O,DE∥CA,AE∥BD.求证:四边形AODE是菱形. 已知如图,O是△ABC内一点,求证:∠AOB=∠1+∠2+∠C.
已知如图,O是△ABC内一点,求证:∠AOB=∠1+∠2+∠C.