题目内容
如图，PA、PB是⊙O的切线，A、B是切点，C是⊙O上一点，若∠P=40°，则∠C=考点：切线的性质
专题：
分析：首先连接OA，OB，由PA、PB是⊙O的切线，∠P=40°，可求得∠AOB的度数，又由圆周角定理，即可求得答案．
解答：
解：连接OB，OA，
∵PA、PB是⊙O的切线，
∴PA⊥OA，PB⊥OB，
∴∠PAO=∠PBO=90°，
∵∠P=40°，
∴∠AOB=360°-∠P-∠PAO-∠PBO=140°，
∴∠C=
∠AOB=70°．
故答案为：70°．
解：连接OB，OA，∵PA、PB是⊙O的切线，
∴PA⊥OA，PB⊥OB，
∴∠PAO=∠PBO=90°，
∵∠P=40°，
∴∠AOB=360°-∠P-∠PAO-∠PBO=140°，
∴∠C=
| 1 |
| 2 |
故答案为：70°．
点评：此题考查了切线的性质以及圆周角定理．此题难度不大，注意掌握辅助线的作法，注意掌握数形结合思想的应用．
练习册系列答案
相关题目
如图，在数轴上有A、B两点，所表示的数分别为a、a+4，A点以每秒3个单位长度的速度向正方向运动，同时B点以每秒1个单位长度的速度也向正方向运动，设运动时间为t秒．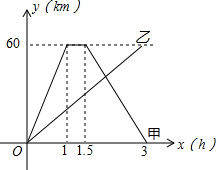
甲、乙两人同时从相距60千米的A地前往B地，甲乘汽车，乙骑摩托车，甲到达B地停留半小时后返回A地，如图是他们离A地的距离y（千米）与时间x（时）之间的函数关系图象．
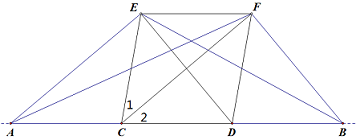如图，点C，D在线段AB上，EF∥AB，CE=CD，∠1=∠2．
如图，小明为了测量其所在位置A点到河对岸B点之间的距离，沿着与AB垂直的方向走了m米，到达点C，测得∠ACB=α，那么AB等于