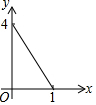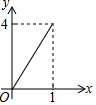题目内容
13.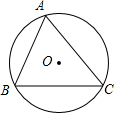 如图,⊙O是△ABC的外接圆,⊙O的半径r=2,sinB=$\frac{3}{4}$,则弦AC的长为( )
如图,⊙O是△ABC的外接圆,⊙O的半径r=2,sinB=$\frac{3}{4}$,则弦AC的长为( )| A. | 4 | B. | 3 | C. | 2 | D. | $\sqrt{3}$ |
分析 连接AO并延长交⊙O于点D,连接CD,由圆周角定理可知∠B=∠D,∠ACD=90°,再由⊙O的半径r=2可以求出AD的长,再由sinB=$\frac{3}{4}$得出CD的长,利用勾股定理即可得出结论.
解答  解:如图,连接AO并延长交⊙O于点D,连接CD,
解:如图,连接AO并延长交⊙O于点D,连接CD,
∵∠B与∠D是同弧所对的圆周角,AD是⊙O的直径,
∴∠B=∠D,∠ACD=90°.
∵⊙O的半径r=2,
∴AD=4.
∵sinB=$\frac{3}{4}$,
∴$\frac{AC}{AD}$=$\frac{3}{4}$,即$\frac{3}{4}$=$\frac{AC}{4}$,
∴AC=3.
故选B.
点评 本题考查的是三角形的外接圆与外心,根据题意构造出直角三角形是解答此题的关键.

练习册系列答案
相关题目
4. 石墨烯(Graphene)是一种由碳原子以sp2杂化轨道组成的六角型呈蜂巢晶格的平面薄膜,是目前发现的厚度最薄、强度最大、导电导热性能最强的一种新型纳米材料,其厚度仅为0.334纳米.数据0.334纳米用科学记数法可以表示为( )
石墨烯(Graphene)是一种由碳原子以sp2杂化轨道组成的六角型呈蜂巢晶格的平面薄膜,是目前发现的厚度最薄、强度最大、导电导热性能最强的一种新型纳米材料,其厚度仅为0.334纳米.数据0.334纳米用科学记数法可以表示为( )
 石墨烯(Graphene)是一种由碳原子以sp2杂化轨道组成的六角型呈蜂巢晶格的平面薄膜,是目前发现的厚度最薄、强度最大、导电导热性能最强的一种新型纳米材料,其厚度仅为0.334纳米.数据0.334纳米用科学记数法可以表示为( )
石墨烯(Graphene)是一种由碳原子以sp2杂化轨道组成的六角型呈蜂巢晶格的平面薄膜,是目前发现的厚度最薄、强度最大、导电导热性能最强的一种新型纳米材料,其厚度仅为0.334纳米.数据0.334纳米用科学记数法可以表示为( )| A. | 0.334×10-9米 | B. | 3.34×10-9米 | C. | 3.34×10-10米 | D. | 3.34×10-8米 |
1.若点(a,b)在一次函数y=2x-3的图象上,则代数式8a-4b+2的值是( )
| A. | -10 | B. | -6 | C. | 10 | D. | 14 |
8.已知二次函数y=ax2-4ax(a>0),小明给出了四个判断:①对称轴是x=2;②图象与坐标轴只有两个交点;③方程ax2-4ax-2=0一定有实数根;④当x≤3时,y随x的增大而减小.其中正确的判断是( )
| A. | ②③④ | B. | ①③④ | C. | ①②④ | D. | ①②③ |
18. 如图,AB∥CD,∠CDE=130°,则∠A的度数是( )
如图,AB∥CD,∠CDE=130°,则∠A的度数是( )
 如图,AB∥CD,∠CDE=130°,则∠A的度数是( )
如图,AB∥CD,∠CDE=130°,则∠A的度数是( )| A. | 130° | B. | 50° | C. | 70° | D. | 30° |
5.下列各数中,最大的是( )
| A. | 0 | B. | 1 | C. | -1 | D. | -$\frac{1}{2}$ |
3.某鞋店一天卖出运动鞋12双,其中各种尺码的鞋的销售量如下表:则这12双鞋的尺码组成的一组数据中,众数和中位数分别是( )
| 码(cm) | 23.5 | 24 | 24.5 | 25 | 25.5 |
| 销售量(双) | 1 | 2 | 2 | 5 | 2 |
| A. | 25,25 | B. | 24.5,25 | C. | 25,24.5 | D. | 24.5,24.5 |
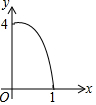
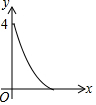
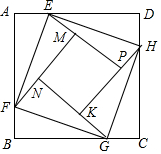 如图正方形ABCD的边长为2,点E,F,G,H分别在AD,AB,BC,CD上,且EA=FB=GC=HD,分别将△AEF,△BFG,△CGH,△DHE沿EF,FG,GH,HE翻折,得四边形MNKP,设AE=x(0<x<1),S四边形MNKP=y,则y关于x的函数图象大致为( )
如图正方形ABCD的边长为2,点E,F,G,H分别在AD,AB,BC,CD上,且EA=FB=GC=HD,分别将△AEF,△BFG,△CGH,△DHE沿EF,FG,GH,HE翻折,得四边形MNKP,设AE=x(0<x<1),S四边形MNKP=y,则y关于x的函数图象大致为( )