题目内容
8.已知二次函数y=ax2-4ax(a>0),小明给出了四个判断:①对称轴是x=2;②图象与坐标轴只有两个交点;③方程ax2-4ax-2=0一定有实数根;④当x≤3时,y随x的增大而减小.其中正确的判断是( )| A. | ②③④ | B. | ①③④ | C. | ①②④ | D. | ①②③ |
分析 根据抛物线的对称轴公式判断①;求出ax2-4ax=0的判别式△=16a2>0,得出图象与x轴有两个交点,又图象过原点,得到图象与坐标轴只有两个交点,即可判断②;计算方程ax2-4ax-2=0的判别式△的值,即可判断③;根据二次函数的增减性判断④.
解答 解:①二次函数y=ax2-4ax(a>0),
∴对称轴是x=$\frac{4a}{2a}$=2,故①正确;
②∵△=16a2>0,
∴图象与x轴有两个交点,
又∵x=0时y=0,即图象过原点,
∴图象与y轴交点是原点,
∴图象与坐标轴只有两个交点,故②正确;
③∵方程ax2-4ax-2=0的判别式△=16a2+8a,而a>0,
∴△>0,
∴方程ax2-4ax-2=0一定有实数根,故③正确;
④∵二次函数y=ax2-4ax(a>0)开口向上,对称轴是x=2,
∴当x<2时,y随x的增大而减小;当x>2时,y随x的增大而增大,
∴当x≤3时,y随x的增大而减小是错误的,故④错误.
故选D.
点评 本题考查了抛物线与x轴的交点,掌握二次函数与一元二次方程的关系、二次函数的性质是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.王师傅每月都开着同一辆油电混合动力汽车从家出发到甲地果园进行志愿服务.纯燃油行驶时,耗油费用80元;纯电动行驶时,耗电费用30元.已知该汽车每行驶1千米,耗油费比耗电费多0.5元,求王师傅家到甲地果园的路程为多少千米?设王师傅家到甲地果园的路程为x千米,根据题意列出的方程是( )
| A. | 80+0.5x=30 | B. | 0.5x-80=30 | C. | $\frac{80}{x}$-0.5=$\frac{30}{x}$ | D. | $\frac{x}{80}$+0.5=$\frac{x}{30}$ |
16. 如图,△ABC内接于⊙O,BD为⊙O的直径,BD与AC相交于点H,AC的延长线与过点B的直线相交于点E,且∠A=∠EBC,作CG∥EB,CG与BD、BA分别相交于点F、G,下列说法中:①CF⊥BD;②BC2=BG•BA;③BC2=BF•BD;④CH=CB.正确的个数是 ( )
如图,△ABC内接于⊙O,BD为⊙O的直径,BD与AC相交于点H,AC的延长线与过点B的直线相交于点E,且∠A=∠EBC,作CG∥EB,CG与BD、BA分别相交于点F、G,下列说法中:①CF⊥BD;②BC2=BG•BA;③BC2=BF•BD;④CH=CB.正确的个数是 ( )
 如图,△ABC内接于⊙O,BD为⊙O的直径,BD与AC相交于点H,AC的延长线与过点B的直线相交于点E,且∠A=∠EBC,作CG∥EB,CG与BD、BA分别相交于点F、G,下列说法中:①CF⊥BD;②BC2=BG•BA;③BC2=BF•BD;④CH=CB.正确的个数是 ( )
如图,△ABC内接于⊙O,BD为⊙O的直径,BD与AC相交于点H,AC的延长线与过点B的直线相交于点E,且∠A=∠EBC,作CG∥EB,CG与BD、BA分别相交于点F、G,下列说法中:①CF⊥BD;②BC2=BG•BA;③BC2=BF•BD;④CH=CB.正确的个数是 ( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
13.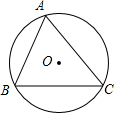 如图,⊙O是△ABC的外接圆,⊙O的半径r=2,sinB=$\frac{3}{4}$,则弦AC的长为( )
如图,⊙O是△ABC的外接圆,⊙O的半径r=2,sinB=$\frac{3}{4}$,则弦AC的长为( )
 如图,⊙O是△ABC的外接圆,⊙O的半径r=2,sinB=$\frac{3}{4}$,则弦AC的长为( )
如图,⊙O是△ABC的外接圆,⊙O的半径r=2,sinB=$\frac{3}{4}$,则弦AC的长为( )| A. | 4 | B. | 3 | C. | 2 | D. | $\sqrt{3}$ |
20.为积极支持鄂州市创建国家卫生城市工作,某商家计划从厂家采购A,B两种清洁产品共20件,产品的采购单价(元/件)是采购数量(件)的相关信息如下表所示.
(1)设B产品的采购数量为x(件),采购单价为y1(元/件),求y1与x的关系式;
(2)经商家与厂家协商,采购A产品的数量不少于B产品数量的$\frac{11}{9}$,且B产品采购单价不高于1250元,求该商家共有几种进货方案?
(3)该商家分别以1760元/件和1700元/件的销售单价售出A,B两种产品,且全部售完,在(2)的条件下,求采购A种产品多少件时总利润最大?并求最大利润.
| 采购数量(件) | 2 | 4 | 6 | … |
| A产品单价(元) | 1460 | 1420 | 1380 | … |
| B产品单价(元) | 1280 | 1260 | 1240 | … |
(2)经商家与厂家协商,采购A产品的数量不少于B产品数量的$\frac{11}{9}$,且B产品采购单价不高于1250元,求该商家共有几种进货方案?
(3)该商家分别以1760元/件和1700元/件的销售单价售出A,B两种产品,且全部售完,在(2)的条件下,求采购A种产品多少件时总利润最大?并求最大利润.
18.$\sqrt{2}$的相反数是( )
| A. | -$\frac{\sqrt{2}}{2}$ | B. | $\sqrt{2}$ | C. | -$\sqrt{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
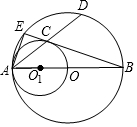 如图,AB是⊙O的直径,AO是⊙O1的直径,⊙O的弦AD交⊙O1于点C,BC的延长线交⊙O于点E.
如图,AB是⊙O的直径,AO是⊙O1的直径,⊙O的弦AD交⊙O1于点C,BC的延长线交⊙O于点E. 加图,已知在数轴上点A表示的数是6,B是数轴上一点,且AB=10,动点P从点A出发,以每秒6个单位长度的速度沿数轴匀速向左运动,设运动时间为t(t>0)秒.
加图,已知在数轴上点A表示的数是6,B是数轴上一点,且AB=10,动点P从点A出发,以每秒6个单位长度的速度沿数轴匀速向左运动,设运动时间为t(t>0)秒.