题目内容
如图，点D，C，A在同一条直线上，在△ABC中，∠A∶∠ABC∶∠ACB＝3∶5∶10，若△EDC≌△ABC，则∠BCE的度数为＿.
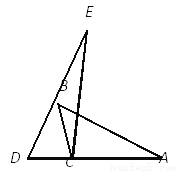
20°
【解析】利用三角形的三角的比∠A：∠ABC：∠ACB=3：5：10，设∠A=3x°，则∠ABC=5x°，∠ACB=10x°，根据三角形的内角和为180°得3x+5x+10x=180，解得x=10，求出三角的度数∠A=30°，∠ABC=50°，∠ACB=100°，可得∠BCN=180°-100°=80°，再由△MNC≌△ABC得到∠ACB=∠MCN=100°，因此可求得∠BCM=∠NC...
练习册系列答案
芒果教辅达标测试卷系列答案
相关题目
平行四边形的周长等于56 cm，两邻边长的比为3∶1，那么这个平行四边形较长的边长为_______.
21cm
【解析】【解析】
∵四边形ABCD是平行四边形，∴AB=CD，AD=BC．
∵平行四边形的周长等于56cm，∴AB+CD+AD+BC=56cm，∴AB+BC=28cm．
∵BC：AB=3：1，∴BC=21cm，AB=7cm，∴这个平行四边形较长的边长为21cm．
故答案为：21cm． 在实数范围内定义一种新运算“⊕”，其运算规则为：a⊕b＝－2a＋3b.如：1⊕5＝－2×1＋3×5＝13.则不等式x⊕4＜0的解集为____.
4
【解析】试题解析：x?4=2x+3×4=0
解得：x=6. 我们知道过n边形的一个顶点可以做（n－3）条对角线，这（n－3）条对角线把三角形分割成（n－2）个三角形，想一想这是为什么？如图1．
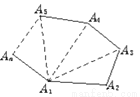
图1
如图2，在n边形的边上任意取一点，连结这点与各顶点的线段可以把n边形分成几个三角形？
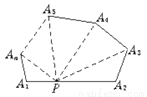
图2
想一想，利用这两个图形，怎样证明多边形的内角和定理．
n-2．想一想见解析
【解析】分析：本题主要考查利用三角形内角和定理来证明多边形的内角和定理，从多边形的一个顶点出发引对角线，则把n边形分成（n-2)个三角形从而证明多边形的内角和定理.
本题解析：
(1)因为对角线是连结不相邻的两个顶点之间的线段，每一个顶点都有两个相邻的顶点，所以有（n-3)条对角线，三条边组成一个三角形，(1)图可分成(n-2)个三角形,
(2)图可分... 一个多边形的内角度数从小到大排列起来，恰好依次增加相同的度数，其中最小角是
，最大角是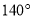
,求这个多边形的边数.
6
【解析】本题考查的是多边形的性质
根据“依次增加相同的度数，其中最小角是，最大角是”即可解得结果，注意边数为正整数。
设多边形的边数是，依次增加，
则
解得符合题意的正整数解
答：这个多边形的边数为 如图，已知在△ABC中，CD是AB边上的高线，BE平分∠ABC，交CD于点E，BC=5，DE=2，则△BCE的面积等于（ ）
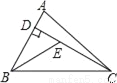
A. 10 B. 7 C. 5 D. 4
C
【解析】作EF⊥BC于F，
∵BE平分∠ABC，ED⊥AB，EF⊥BC，
∴EF=DE=2，
∴S△BCE=BC?EF=×5×2=5，
故选C. 一项工程，甲工程队单独完成需要m天，乙工程队单独完成比甲队单独完成多需要n天时间，那么甲、乙工程队合做需要多少天能够完成此项工程？
【解析】本题考查的是根据实际问题列分式
根据工作时间即可表示出工作效率，从而得到结果。
由题意得，甲的工作效率为，乙的工作效率为，
则甲、乙工程队合做的时间为 计算：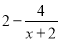 
= ．
【解析】试题分析：原式＝
＝
＝．
故答案为： ． 从一副扑克牌中任取一张，则抽到红桃的频率与抽到黑桃的频率哪个大？抽到梅花与抽到大、小王的频率哪个大？
抽到红桃的可能性与抽到黑桃的频率一样大，而抽到梅花的频率大于抽到大、小王的频率.
【解析】试题分析: 本题考察可能性大小的应用，关键是根据各色扑克的张数求出各色扑克被抽到的频率是多少.
【解析】
一副扑克牌有54张，其中红桃、黑桃、梅花、方块各13张，大、小王各一张，所以，抽到红桃的的频率为，抽到黑桃的的频率为，抽到梅花的的频率为，抽到大、小王的的频率为. 所以抽到红桃的可能性与抽到...