题目内容
在四边形ABCD中，∠A＝∠C＝90°，∠B与∠D的度数比是3：2，求∠B，∠D的度数．
∠B＝108°，∠D＝72°．
【解析】分析：由已知∠A=∠C=90°,较易得到∠B+∠D=180°,再根据已知的∠B:∠D=3:2,即可求解.
本题解析：
∵∠ A ＋∠ C ＝90°＋90°＝180°，∴∠ B ＋∠ D ＝360°－(∠ A ＋∠ C )＝360°－1 80°＝180°．设∠ B ＝( 3 x )°，则∠ D ＝(2 x )°，∴(3 x )°＋(2 x )...
练习册系列答案
小学课时作业全通练案系列答案
金版课堂课时训练系列答案
单元全能练考卷系列答案
新黄冈兵法密卷系列答案
相关题目
如图所示，E，F分别为平行四边形ABCD中AD，BC的中点，G，H在BD上，且 BG＝DH，求证四边形EGFH是平行四边形．
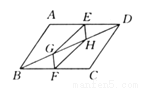
答案见解析
【解析】试题分析：由四边形ABCD是平行四边形，得到AD=BC，AD∥BC，由AD∥BC，得到∠ADB=∠DBC，因为E、F分别为?ABCD的边AD、BC的中点，得到DE=BF，由三角形全等证得EH=FG，∠EHD=∠FGB，得到EH∥FG，证出四边形FGEH是平行四边形．
试题解析：证明：∵四边形ABCD是平行四边形，∴AD=BC，AD∥BC，∴∠ADB=∠DBC．∵E、... 下列条件中，能判别四边形是平行四边形的是 ( )
A. 一组对边相等，另一组对边平行 B. 一组对边平行，一组对角互补
C. 一组对角相等，一组邻角互补 D. 一组对角互补，另一组对角相等
C
【解析】解：A．一组对边相等，另一组对边平行，也有可能是等腰梯形；
B．一组对边平行，一组对角互补，也有可能是等腰梯形；
C．一组对角相等，一组邻角互补可得到两组对角分别相等，所以是平行四边形；
D．一组对角互补，另一组对角相等，可能是含两个直角的一般四边形．
故选C． 下列各式中，是一元一次不等式的是（ ）
A. 5+4＞8 B. 2x－1 C. 2x≤5
D. 
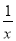－3x≥0
C
【解析】试题解析：A、是不等式，但不是一元一次不等式，故本选项错误；
B、是一元一次方程，不是一元一次不等式，故本选项错误；
C、是一元一次不等式，故本选项正确；
D、不是一元一次不等式，故本选项错误；
故选C． 我们知道过n边形的一个顶点可以做（n－3）条对角线，这（n－3）条对角线把三角形分割成（n－2）个三角形，想一想这是为什么？如图1．
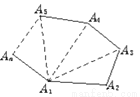
图1
如图2，在n边形的边上任意取一点，连结这点与各顶点的线段可以把n边形分成几个三角形？
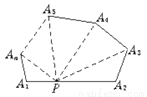
图2
想一想，利用这两个图形，怎样证明多边形的内角和定理．
n-2．想一想见解析
【解析】分析：本题主要考查利用三角形内角和定理来证明多边形的内角和定理，从多边形的一个顶点出发引对角线，则把n边形分成（n-2)个三角形从而证明多边形的内角和定理.
本题解析：
(1)因为对角线是连结不相邻的两个顶点之间的线段，每一个顶点都有两个相邻的顶点，所以有（n-3)条对角线，三条边组成一个三角形，(1)图可分成(n-2)个三角形,
(2)图可分... 如图，在△ABC和△ADC中，下列论断：①AB＝AD；②∠ABC＝∠ADC＝90°；③BC＝DC．把其中两个论断作为条件，另一个论断作为结论，可以写出＿个真命题．
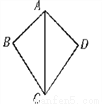
2
【解析】根据题意，可得三种命题，由①②③，根据直角三角形全等的判定HL可证明，是真命题；由①③②，能证明∠ABC=∠ADC，但是不能得出一定是90°，是假命题；由②③①，根据SAS可证明两三角形全等，再根据全等三角形的性质可证明，故是真命题.因此可知真命题有2个.
故答案为：2. 如图，已知在△ABC中，CD是AB边上的高线，BE平分∠ABC，交CD于点E，BC=5，DE=2，则△BCE的面积等于（ ）
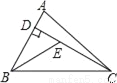
A. 10 B. 7 C. 5 D. 4
C
【解析】作EF⊥BC于F，
∵BE平分∠ABC，ED⊥AB，EF⊥BC，
∴EF=DE=2，
∴S△BCE=BC?EF=×5×2=5，
故选C. 当分式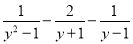
的值等于零时，则y=_________．
【解析】试题分析：当分式的值等于零时，
＝0，
去分母得：1－2(y－1)－(y＋1)＝0，
解得：y＝，
当y＝时y2－1≠0，
所以y＝是分式方程的解，
故答案为： ． 在△MNB中，BN=6，点A，C，D分别在MB，NB，MN上，四边形ABCD为平行四边形，且∠NDC=∠MDA，则四边形ABCD的周长是（ ）
A．24 B．18 C．16 D．12
D
【解析】
在平行四边形ABCD中CD∥AB，AD∥BC，∴∠M=∠NDC，∠N=∠MDA，∵∠NDC=
∠MDA，∴∠M=∠N=∠NDC=∠MDA，∴MB=BN=6，CD=CN，AD=MA，∴四边形ABCD的周长=AB+BC+CD+AD=MA+AB+BC+CN=MB+BN=2BN=12．