题目内容
 如图,△ABC的两条高分别为BE、CF,M为BC的中点.求证:ME=MF.
如图,△ABC的两条高分别为BE、CF,M为BC的中点.求证:ME=MF.考点:直角三角形斜边上的中线
专题:证明题
分析:根据直角三角形斜边上的中线等于斜边的一半可得ME=
BC,MF=
BC,从而得证.
| 1 |
| 2 |
| 1 |
| 2 |
解答:证明:∵BE是△ABC的高,M为BC的中点,
∴ME=
BC,
∵CF是△ABC的高,M为BC的中点,
∴MF=
BC,
∴ME=MF.
∴ME=
| 1 |
| 2 |
∵CF是△ABC的高,M为BC的中点,
∴MF=
| 1 |
| 2 |
∴ME=MF.
点评:本题考查了直角三角形斜边上的中线等于斜边的一半的性质,熟记性质是解题的关键.

练习册系列答案
相关题目
请判断下列各组是二元一次方程组
的解是( )
|
A、
| |||||
B、
| |||||
C、
| |||||
D、
|
若实数x满足x+
-1=0,则
的值为( )
| 2x |
| 3x2 |
| x4+x2+1 |
A、
| ||
B、
| ||
| C、5 | ||
D、
|
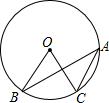 如图,在⊙O中,∠BOC=60°,则∠BAC等于( )
如图,在⊙O中,∠BOC=60°,则∠BAC等于( )| A、60° | B、50° |
| C、40° | D、30° |
 在平面直角坐标系中,一次函数y=kx+b的图象与x轴、y轴分别相交于A(-3,0),B(0,-3)两点,二次函数y=x2+mx+n的图象经过点A.
在平面直角坐标系中,一次函数y=kx+b的图象与x轴、y轴分别相交于A(-3,0),B(0,-3)两点,二次函数y=x2+mx+n的图象经过点A.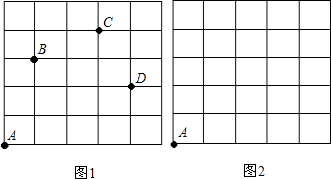
 在平面直角坐标系xOy中,点M(
在平面直角坐标系xOy中,点M(
 已知数a,b在数轴上的位置如图,化简
已知数a,b在数轴上的位置如图,化简